seaborn regression

很多数据集包含多个数字变量，分析的目标通常是把这些变量关联起来。之前介绍了通过展示两个变量的联合分布来实现这一目标的函数。尽管如此，使用统计模型来估计两组杂乱的观测之间的简单关系仍然很有帮助。本章讨论的函数通过线性回归的常用框架完成上述任务

遵循Turkey的理念，seaborn的回归图主要想增加一种视觉指导，有助于在探索性数据分析的过程中突出数据的模式。这就是说，seaborn本身不是用于统计分析的。要想获得与拟合回归模型相关的数量测度需要使用statsmodels。然而，seaborn的目标是通过快速简便的可视化对数据集进行探索，这与通过统计表对数据集进行探索一样重要

1
2
3
4
5
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
sns.set_theme(color_codes=True)
tips = sns.load_dataset('tips')

绘制线性回归模型的函数

Seaborn中有两个主要的函数用来绘制回归获得的线性关系。regplot()和lmplot()这两个函数密切相关，有很多相同的核心功能。然而，理解这两个函数的不同也很重要，这样才能根据特定目的快速选择正确的工具

使用最简单的调用命令，两个函数都会绘制两个变量x和y的散点图，拟合回归模型y ~ x，绘制回归线和95%置信区间：

1
sns.regplot(x='total_bill', y='tip', data=tips)

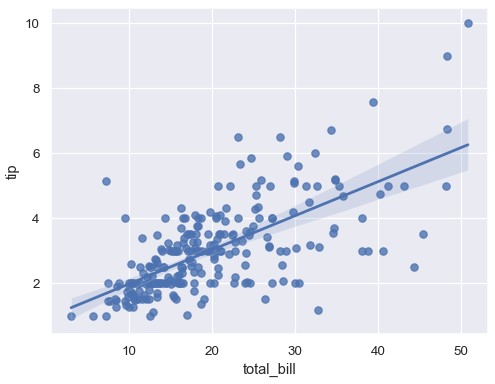
1
sns.lmplot(x='total_bill', y='tip', data=tips)

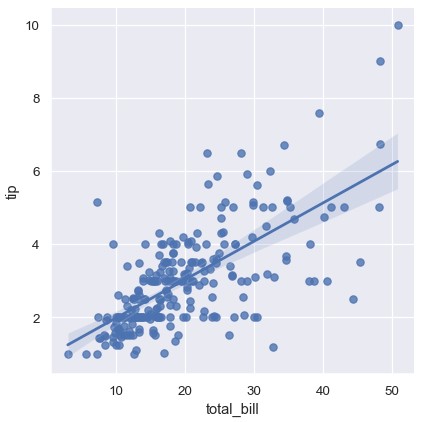
两个函数绘制的图像类似，但是图的形状不同。稍后会解释造成这一现象的原因。现在，需要记住的另一个主要区别是regplot()接受各种格式的x和y变量，包括简单的numpy数组，pandas的Series对象，或者传递给data参数的数据框中的变量名。相反，lmplot()中data是必须参数，x和y参数只能是字符串。这种数据格式称为长数据或者干净数据。除了输入格式更加灵活，regplot()拥有一部分lmplot()的功能，因此将使用后者进行举例说明

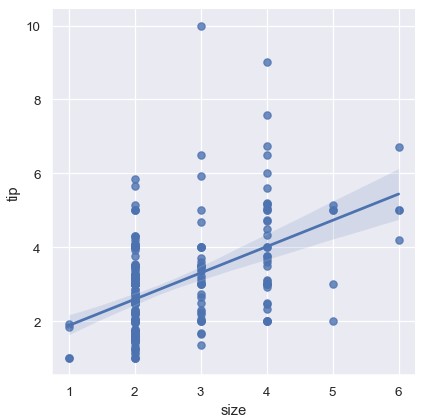
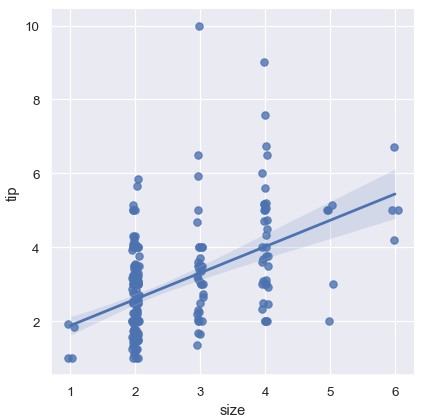
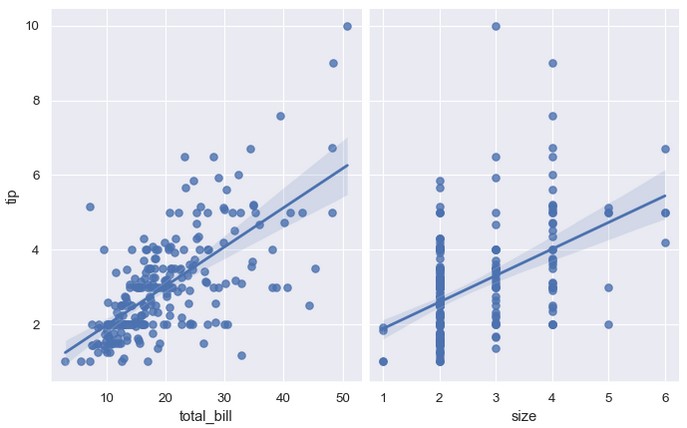
如果一个变量的值是离散的，也可以进行线性回归，只是这种数据集画出的简单散点图不太好看：

1
sns.lmplot(x='size', y='tip', data=tips)

一种办法是向离散值添加随机扰动，使点的分布更加清楚。注意，扰动只针对散点图，并不影响线性回归：

1
sns.lmplot(x='size', y='tip', data=tips, x_jitter=0.05)

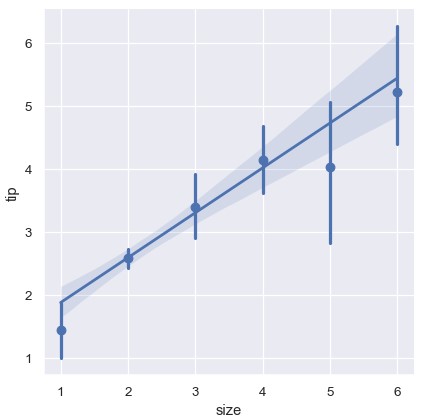
另一种方法是整合每一个离散值对应的观测，绘制其中心趋势的估计和置信区间：

1
sns.lmplot(x='size', y='tip', data=tips, x_estimator=np.mean)

拟合不同类型的模型

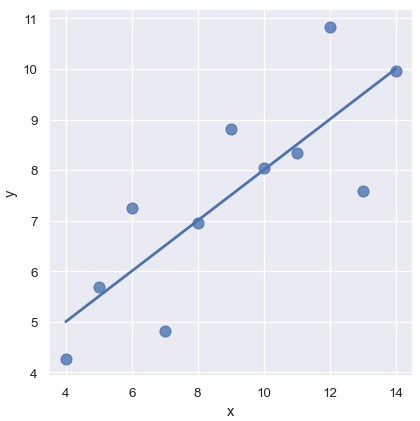
上面使用的简单线性回归模型很容易拟合，然而并不适用于所有数据集。Anscombe’s quartet数据集提供了一些案例，这些案例中简单线性回归的结果完全相同，但数据之间的关系存在肉眼可见的不同。例如，在第一个例子中，线性回归是一个不错的模型：

1
2
anscombe = sns.load_dataset('anscombe')
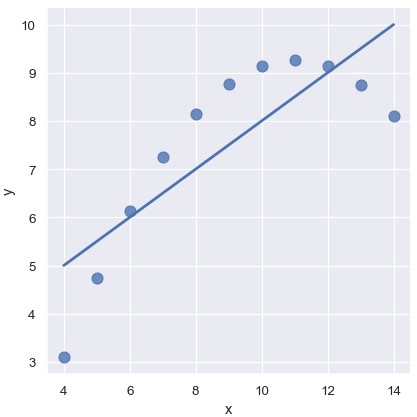
sns.lmplot(x='x', y='y', data=anscombe.query("dataset == 'I'"), ci=None, scatter_kws={'s': 80})

线性关系在第二个数据集中也是一样的，但是明显看出这不是一个好的模型：

1
sns.lmplot(x='x', y='y', data=anscombe.query("dataset == 'II'"), ci=None, scatter_kws={'s': 80})

在展示这类高阶关系时，lmplot()和relplot()可以拟合多项式回归模型来探索数据集中简单的非线性趋势：

1
sns.lmplot(x='x', y='y', data=anscombe.query("dataset == 'II'"), order=2, ci=None, scatter_kws={'s': 80})

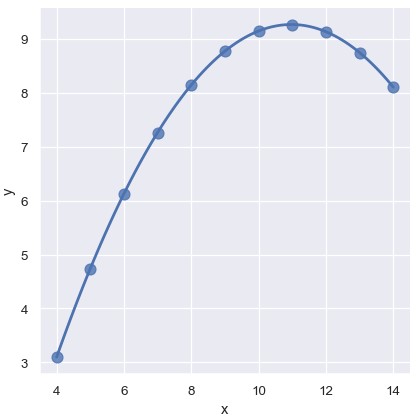
另一个问题是由偏离数据主要趋势的异常值造成的：

1
sns.lmplot(x='x', y='y', data=anscombe.query("dataset == III"), ci=None, scatter_kws={'s': 80})

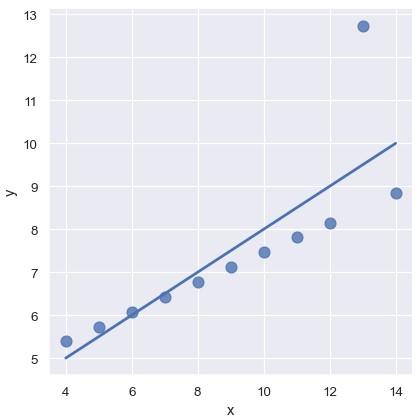
当出现异常值时，鲁棒回归 (robust regression)很有用，它使用一个不同的损失函数来降低大残差的权重：

1
sns.lmplot(x='x', y='y', data=anscombe.query("dataset == 'III'"), robust=True, ci=None, scatter_kws={'s': 80})

如果y变量是二元的，简单线性回归也不会报错，但产生的预测没有意义：

1
2
tips['big_tip'] = (tips.tip / tips.total_bill) > 0.15
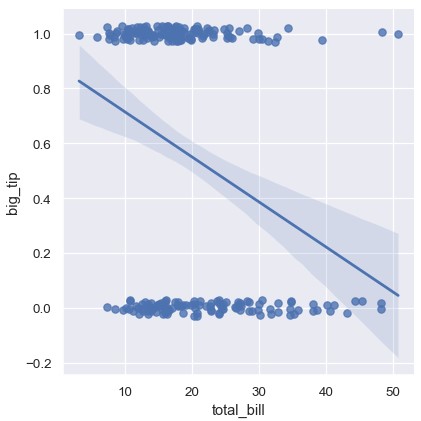
sns.lmplot(x='total_bill', y='big_tip', data=tips, y_jitter=0.03)

这种情况的解决方案是拟合逻辑回归模型，回归线展示的估计是针对每个x值，y = 1的概率：

1
sns.lmplot(x='total_bill', y='big_tip', data=tips, logistic=True, y_jitter=0.03)

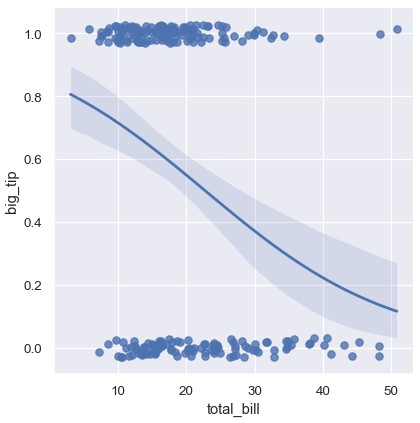
注意，逻辑回归通常比简单线性回归需要更多算力，由于置信区间是使用自举法计算的，可以设置ci=None取消置信区间的计算来加速迭代

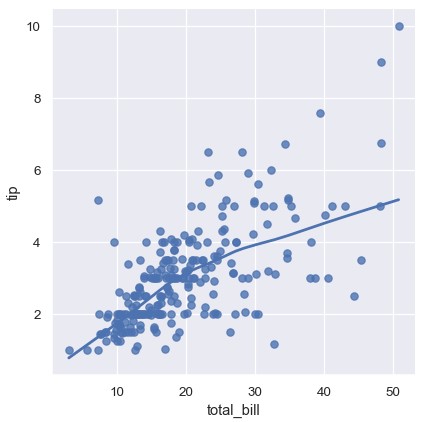
一种完全不同的方法是使用局部加权回归散点平滑 (lowess smoother)拟合非参回归。这种方法的假设最少，但是计算量大，因此目前没有设置置信区间的计算：

1
sns.lmplot(x='total_bill', y='tip', data=tips, lowess=True)

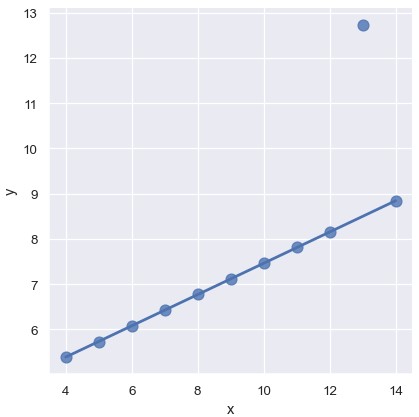
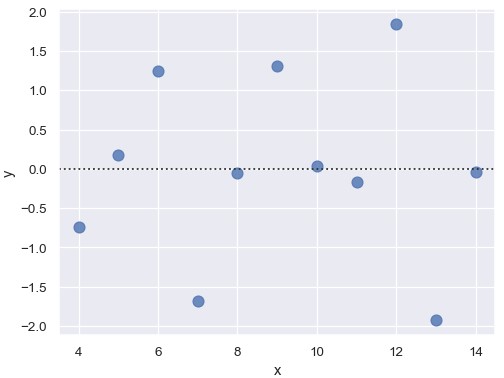
residplot()函数可用于检查简单回归模型是否适用于该数据集。这个函数拟合简单线性模型，然后绘制每个观测的残差。理想情况下，这些值应该随机分布在y = 0附近：

1
sns.residplot(x='x', y='y', data=anscombe.query("dataset == 'I'"), scatter_kws={'s': 80})

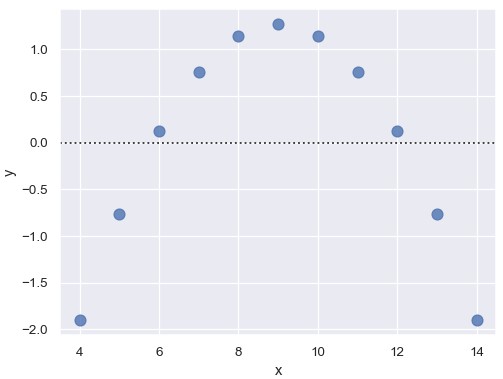
如果残差的分布存在某种结构，说明简单线性回归不适用：

1
sns.lmplot(x='x', y='y', data=anscombe.query("dataset == 'II'"), scatter_kws={'s': 80})

调整其它变量

上面那些图片展示了探索两个变量之间关系的多种方法。然而，更有意义的问题通常是“这两个变量之间的关系如何随第三个变量的取值发生变化”。这就是regplot()和lmplot()的不同之处了。虽然regplot()也能展示一个相互关系，lmplot()结合了regplot()和FacetGrid，便于通过分面展示线性回归，从而能够探索至多三个额外类别型变量的交互作用

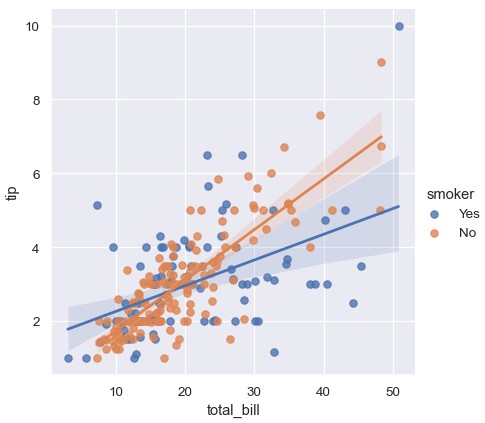
拆分一个相互关系最好的方法是将变量的两个取值绘制在同一个轴上，用不同颜色加以区分：

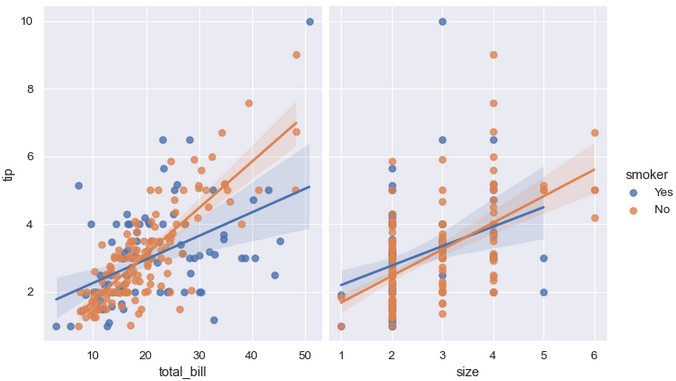
1
sns.lmplot(x='total_bill', y='tip', hue='smoker', data=tips)

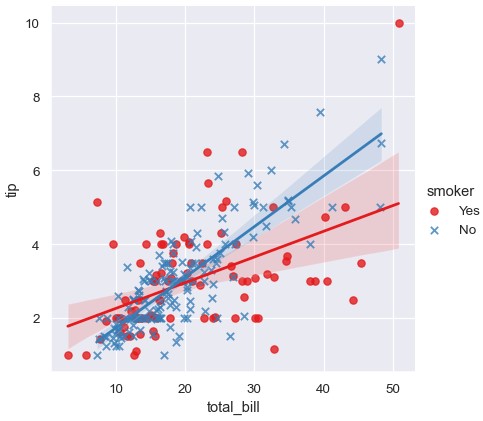
使用不同的散点图记号在黑白图像中也能对类别加以区分。也可以同时使用不同颜色：

1
sns.lmplot(x='total_bill', y='tip', hue='smoker', data=tips, markers=['o', 'x'], palette='Set1')

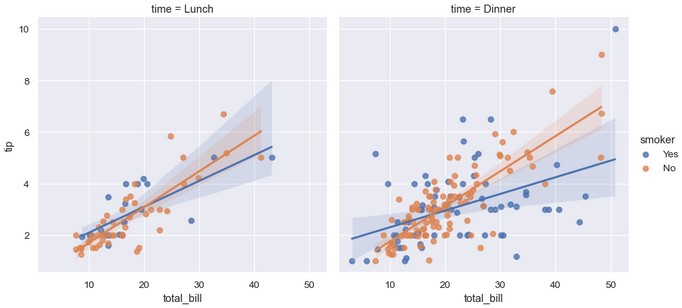
要想再增加一个变量，可以绘制多个“分面” (facets)，变量的每个取值都会单独绘制在格子的行或者列中：

1
sns.lmplot(x='total_bill', y='tip', hue='smoker', col='time', data=tips)

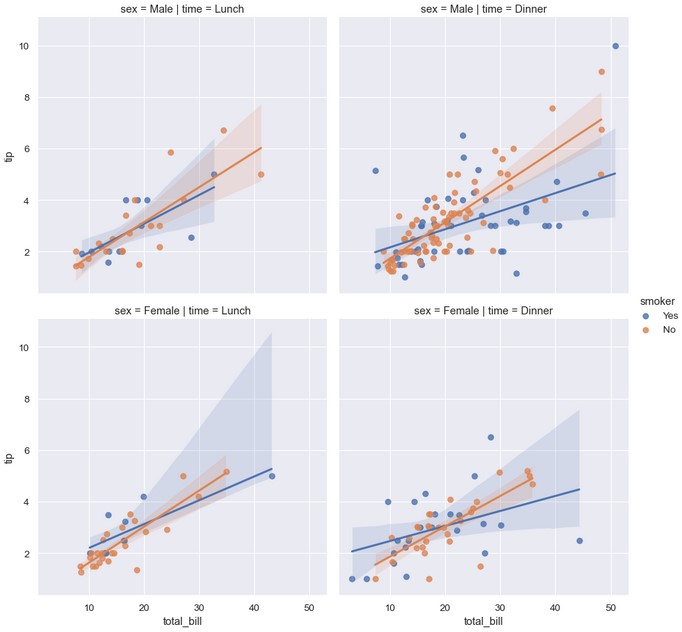
1
sns.lmplot(x='total_bill', y='tip', hue='smoker', col='time', row='sex', data=tips)

控制图片的大小和形状

前面我们注意到，regplot()和lmplot()绘制的图像看起来一样，但形状大小不同。这是因为regplot()是轴水平函数，在特定的轴上进行绘制。这意味着你可以自行制作带有多个面板的组图，精确控制回归图的位置。如果没有明确提供轴对象，regplot()会在当前活跃的轴上进行绘制，这就是为什么默认设置画出的图片与大多数其它matplotlib函数绘制的图片形状大小相同。要想改变图的大小，需要先创建一个图对象：

1
2
f, ax = plt.subplots(figsize=(5, 6))
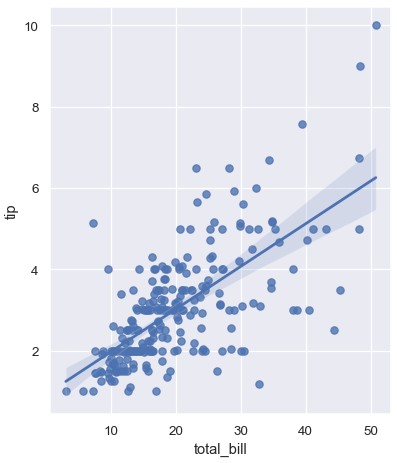
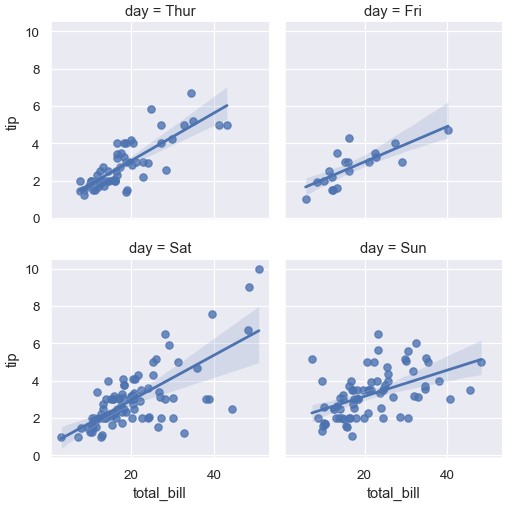
sns.regplot(x='total_bill', y='tip', data=tip, ax=ax)

相反，lmplot()图的形状大小是用height和aspect参数通过FacetGrid界面进行控制的，改变的是每个子图的大小，而不是整个图的大小：

1
sns.lmplot(x='total_bill', y='tip', col='day', data=tips, col_wrap=2, height=3)

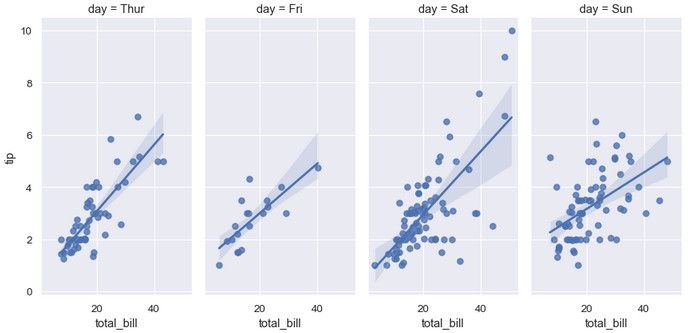
1
sns.lmplot(x='total_bill', y='tip', col='day', data=tips, aspect=0.5)

在其它情境下绘制回归

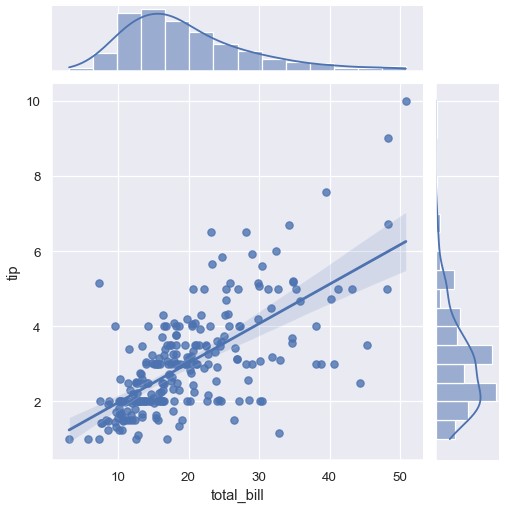
一些其它seaborn函数在更大更复杂的图中使用regplot()。首先是在分布型教程中介绍过的jointplot()。除了之前讨论过的绘图风格，jointplot()可以通过kind='reg'参数在联合分布轴上展示线性回归拟合：

1
sns.jointplot(x='total_bill', y='tip', data=tips, kind='reg')

在pairplot()函数中设置kind='reg'会将regplot()和PairGrid结合起来，展示数据集中变量之间的线性关系。要注意这种方法与lmplot()的不同。在下图中，两个子图展示的不是两个变量在第三个变量取不同值时的关系，而是数据集中两对不同的变量之间的关系：

1
sns.pairplot(tips, x_vars=['total_bill', 'size'], y_vars=['tip'], height=5, aspect=0.8, kind='reg')

与lmplot()类似，可以使用hue参数向pairplot()添加额外的类别型变量：

1
sns.pairplot(tips, x_vars=['total_bill', 'size'], y_vars=['tip'], hue='smoker', height=5, aspect=0.8, kind='reg')