seaborn分布模块

seaborn distributions

在分析数据或者对数据进行建模之前，应该先理解变量是如何分布的。对数据分布进行可视化的技术能够快速回答很多关键问题。数据覆盖多大范围？数据的中心趋势怎么样？是不是严重地向某个方向偏斜？是不是存在双峰的迹象？是不是有明显的异常值？这些问题的答案会根据其它变量定义的子集而有所不同吗？

分布模块包含一些能够回答上述问题的函数。轴水平的函数包括histplot()，kdeplot，ecdfplot()和rugplot()。这些轴水平函数汇集成图水平函数displot()，jointplot()和pairplot()

可视化数据分布的方法很多，每一种都既有优点也有缺点。理解了各种方法的优缺点才能根据特定目标选择最好的可视化方案

绘制单变量直方图

最常见的可视化数据分布的方法也许是直方图。直方图是displot()的默认方法，底层代码与histplot()相同。直方图是一种条形图，代表数据变量的轴被划分成一系列离散的区间，使用条形的长度表示落入每个区间的观测的数量：

penguins = sns.load_dataset('penguins')
sns.displot(penguins, x='flipper_length_mm')

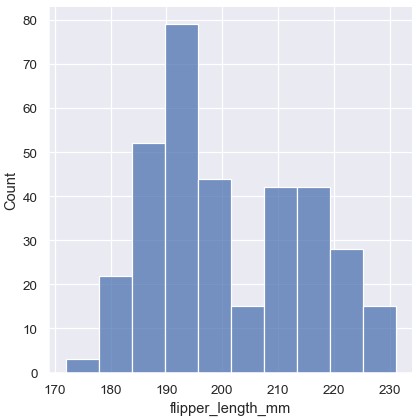
这个图片直接提供了一些关于flipper_length_mm变量的新视角。比如，最常见的鳍状肢长度大约是195mm，但是数据的分布似乎是双峰的，因此这个数值并不能很好地代表所有数据

选择分箱大小

分箱大小是一个很重要的参数，错误的分箱大小会掩盖数据的重要特征，或者使随机变量看起来出现明显特征。displot() / histplot()默认会根据数据的变化幅度及观测的数量自动选择分箱大小。不要过度依赖这些默认设置，因为这依赖于对数据结构的特定假设。建议检查设置不同分箱大小时，数据的分布看起来是不是一致的。使用binwidth参数选择分箱大小：

sns.displot(penguins, x='flipper_length_mm', binwidth=3)

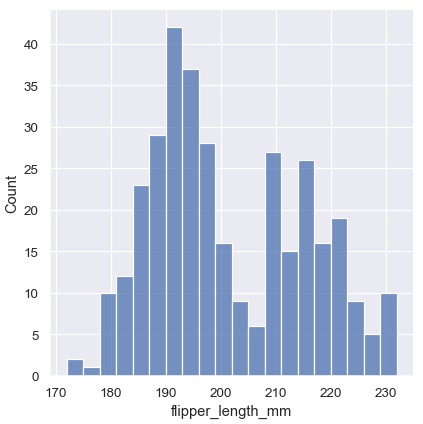
在其它情况下，指定分箱的个数可能比指定分箱的大小更有意义：

sns.displot(penguins, x='flipper_length_mm', bins=20)

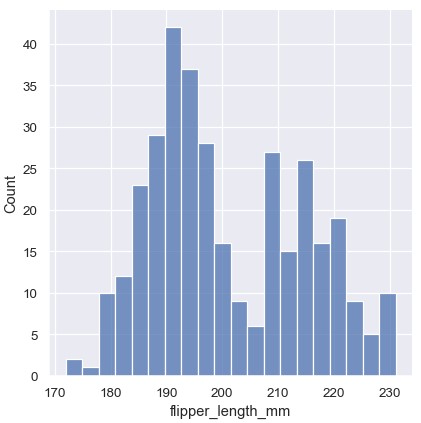
当一个变量的取值中整数的数量非常少时，默认设置可能会出问题。在这种情况下，默认的分箱宽度会非常小，在分布图上产生奇怪的缺口：

tips = sns.load_dataset('tips')
sns.displot(tips, x='size')

一种方法是向bins参数传递一个数组，精确指定分箱的位置：

sns.displot(tips, x='size', bins=[1, 2, 3, 4, 5, 6, 7])

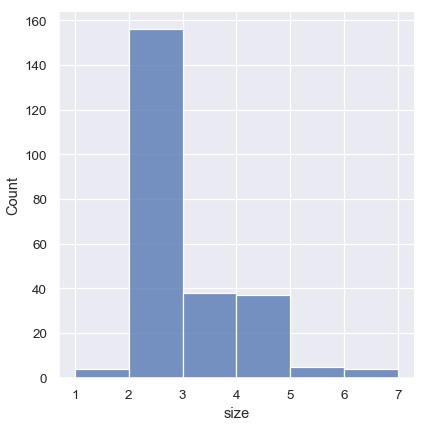
也可以设置discrete=True，选择数据集中的唯一值作为分箱的位置，并且把对应的条形居中摆放到这些位置：

sns.displot(tips, x='size', discrete=True)

利用直方图也可以对类别型变量进行可视化。类别型变量会默认进行离散分箱，可以使用shrink参数将每一个条形的宽度缩小一点，有助于突出类别型变量的特征：

sns.displot(tips, x='day', shrink=0.8)

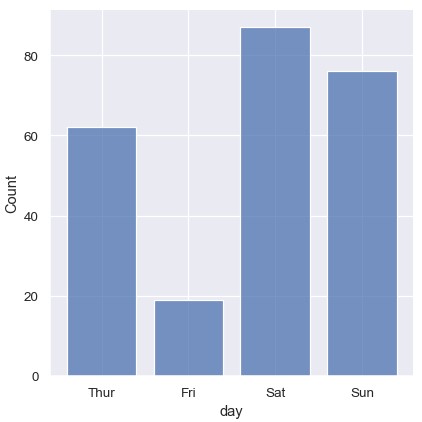
调整其它变量

一旦理解了一个变量的分布，下一个问题通常就是这个变量的分布特征是否随数据集中其它变量的取值而有所不同。例如，是什么造成了上面图中鳍状肢长度的双峰分布？displot()和histplot()支持通过hue语义将数据划分子集。设置hue参数会分别绘制色调变量每种取值的直方图，并通过颜色进行区分：

sns.displot(penguins, x='flipper_length_mm', hue='species')

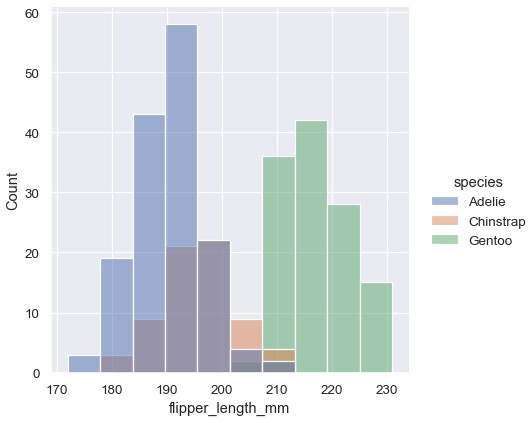
默认情况下，各个直方图一层叠在另一层上面，有时候会难以区分。将直方图的元素从条形改成阶梯状 (step)是一种解决方案：

sns.displot(penguins, x='flipper_length_mm', hue='species', element='step')

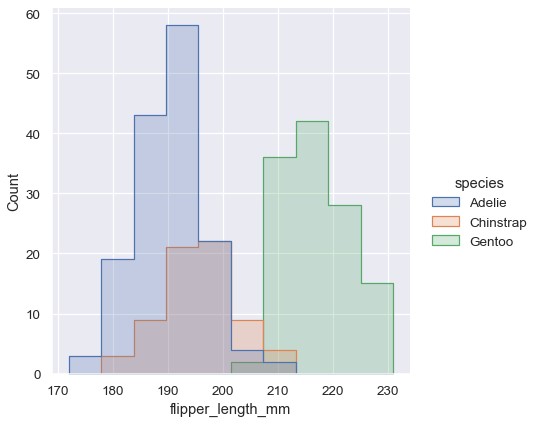
除了把直方图一层一层叠放，还可以把它们在竖直方向上堆积起来。这种情况下，整个直方图的轮廓与单变量直方图的轮廓是一致的：

sns.displot(penguins, x='flipper_length_mm', hue='species', multiple='stack')

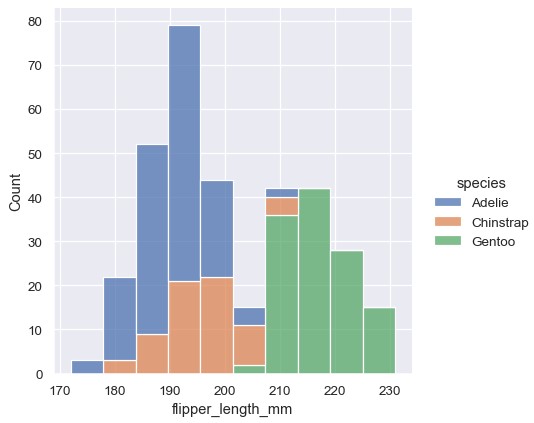
堆积直方图强调变量间整体-部分的关系，但也可能掩盖一些特征 (例如，很难从图中捕捉Adelie企鹅的分布模式)。另一种选择是把各个条形缩减宽度，在水平方向上并列排放。这种方式确保了没有重叠，各个条形的高度仍然是可以互相比较的。对于类别型变量来说，这种方式只适用于取值较少的情况：

sns.displot(penguins, x='flipper_length_mm', hue='sex', multiple='dodge')

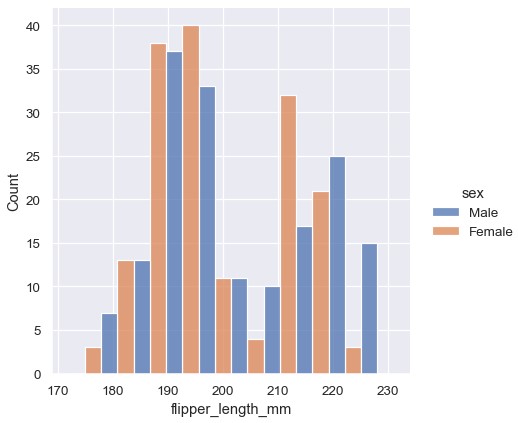
由于displot()是图水平函数，绘制在FacetGrid对象上，因此也可以不设置色调语义，而是把第二个变量赋值给col或者row，将数据子集的分布绘制在单独的子图上。这种方式能很好地展示各个子集的分布，但是很难直接比较：

sns.displot(penguins, x='flipper_length_mm', col='sex')

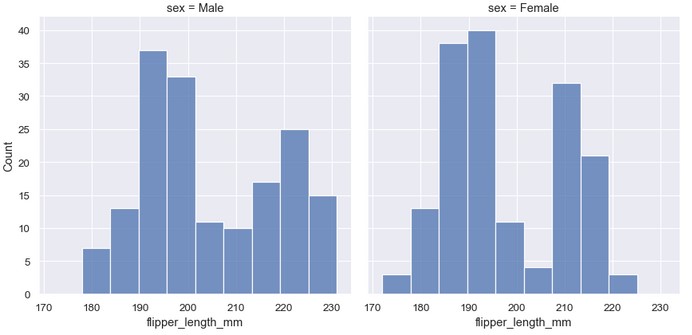
这些方法都不是完美的，稍后将介绍可替代直方图、更适合于比较的备选方案

标准化直方图统计

当各个子集中包含的观测数量不等时，根据计数对它们的分布进行比较可能不太合适。一种解决方案就是使用stat参数将计数进行标准化：

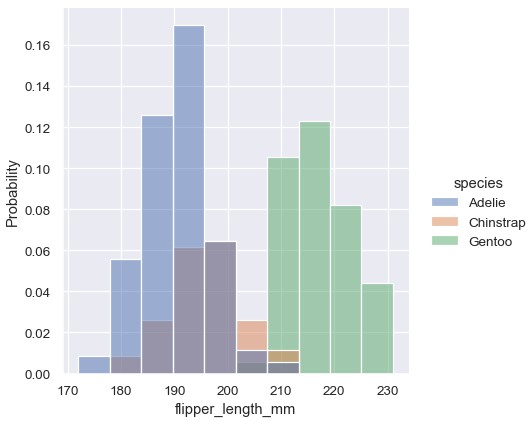
sns.displot(penguins, x='flipper_length_mm', hue='species', stat='density')

然而，在默认情况下，标准化是针对整个数据集进行的，所以只是对条形的高度进行了缩放。设置common_norm=False可以对各个子集分别进行标准化：

sns.displot(penguins, x='flipper_length_mm', hue='species', stat='density', common_norm=False)

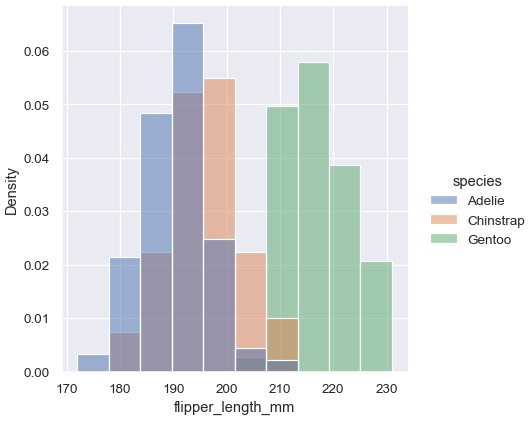
通过密度标准化缩放，所有条形的总面积为1。这样一来，密度轴不再是可以直接解读的。另一种方法是通过标准化使得所有条形的总高度为1。这在变量不连续的情况下最有用，但也可以用于所有的直方图：

sns.displot(penguins, x='flipper_length_mm', hue=
'species', stat='probability')

核密度估计

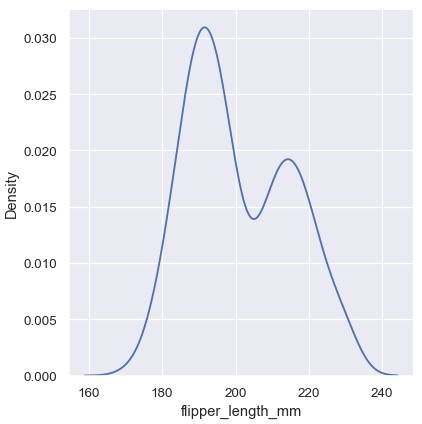
直方图通过分箱和计数，旨在拟合数据背后的概率密度函数。概率密度估计 (KDE)提供了解决这个问题的另一种方案。相比于离散的分箱，KDE使用高斯核对数据的分布进行平滑处理，产生连续的密度估计：

sns.displot(penguins, x='flipper_length_mm', kind='kde')

选择进行平滑处理时的带宽

与直方图的分箱大小类似，KDE是否能够精确表征数据分布取决于进行平滑处理时的带宽。过度平滑的估计可能会抹除一些有意义的特征，而不够平滑的估计会掩盖随机噪声里的真实形状。要想检验估计的鲁棒性，最容易的办法是调整默认带宽：

sns.displot(penguins, x='flipper_length_mm', kind
='kde', bw_adjust=0.25)

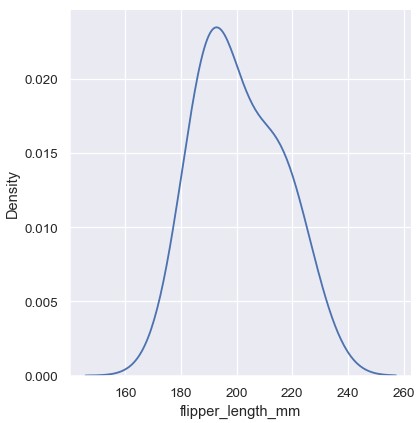
注意，窄一点的带宽使得双峰分布更明显，但是线条不那么平滑。相反，较宽的带宽几乎完全掩盖了双峰分布：

sns.displot(penguins, x='flipper_length_mm', kind='kde', bw_adjust=2)

调整其它变量

与直方图类似，设置hue变量可以针对该变量的每一个取值单独计算密度估计：

sns.displot(penguins, x='flipper_length_mm', hue='species', kind='kde')

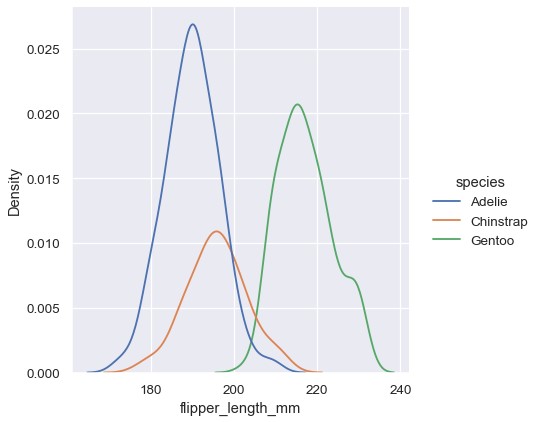
在很多情况下，逐层绘制的KDE比逐层绘制的直方图更容易解读，所以在用于比较时KDE往往是更好的选择。很多类似的绘制多个分布的方案也同样适用于KDE，然而：

sns.displot(penguins, x='flipper_length_mm', hue='species', kind='kde', multiple='stack')

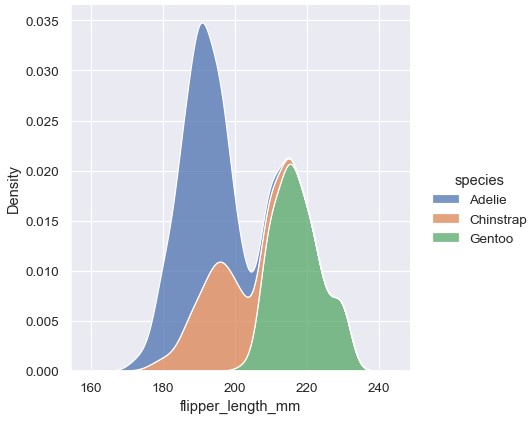
注意在默认条件下堆积图是如何对各条曲线围成的区域进行填色的。也可以对逐层绘制的KDE单独进行填色，使得每个密度估计更容易分辨，虽然默认的透明度会有所不同：

sns.displot(penguins, x='flipper_length_mm', hue='species', kind='kde', fill=True)

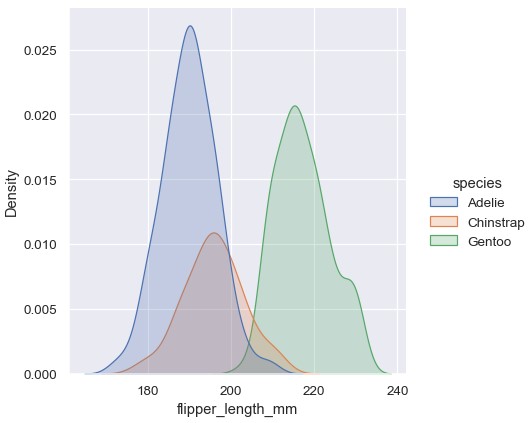
核密度估计陷阱

KDE图有很多优点。便于观察出数据的重要特征 (中心趋势、双峰分布、偏斜情况)，并且很容易将各个子集进行比较。但是也有一些情况KDE难以展现数据背后的特征。这是因为KDE的逻辑是假设数据的分布是平滑的、无界的。如果一个变量的取值本身是有界的，这一假设就会失效。如果有些观测非常接近取值边界 (例如，很小的非负数)，KDE曲线会延伸到不切实际的取值：

sns.displot(tips, x='total_bill', kind='kde')

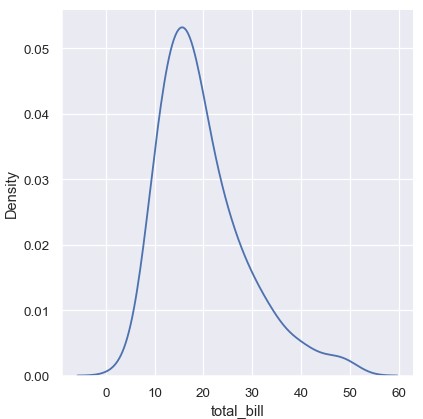
使用cut参数指定曲线可以超出数据极值延伸到多远能够在一定程度上避免这样的问题。但是，这样设置只是影响绘制曲线的范围，密度估计仍然是按照数据无边界的情况进行平滑处理的，导致在数据的极值附近估计偏低：

sns.displot(tips, x='total_bill', kind='kde', cut=0)

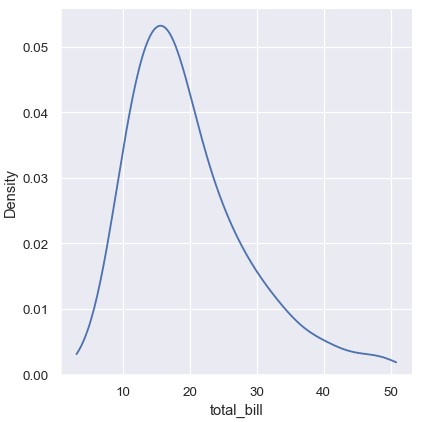
对于离散型数据或者数据本身是连续的，但是有些取值数量极大的情况下，KDE也会失效。要牢记，KDE总是会展示一条平滑的曲线，即使数据本身并不平滑。例如，钻石重量的分布：

diamonds = sns.load_dataset('diamonds')
sns.displot(diamonds, c='carat', kind='kde')

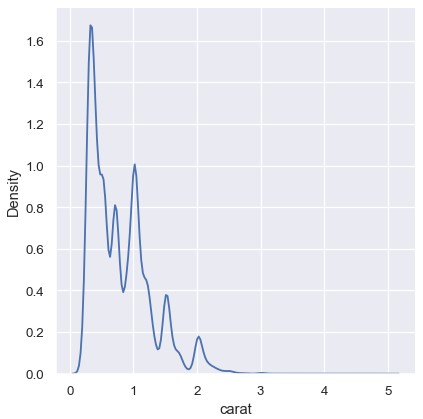
尽管KDE图在特定取值附近形成了一些峰，但直方图展示了更加参差不齐的分布：

sns.displot(diamonds, x='carat')

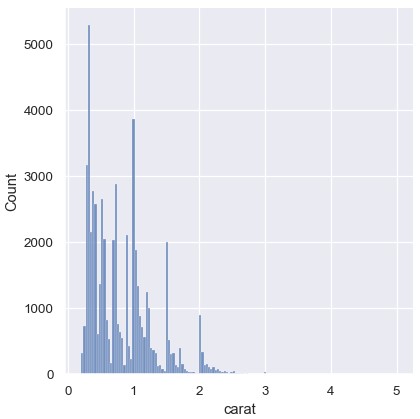
把直方图和KDE结合起来可以作为一种折中的方案。在直方图模式中，displot() (histplot()也是一样)包含了显示平滑后的KDE曲线的选项 (注意，是kde=True而不是kind=kde)：

sns.displot(diamonds, x='carat', kde=True)

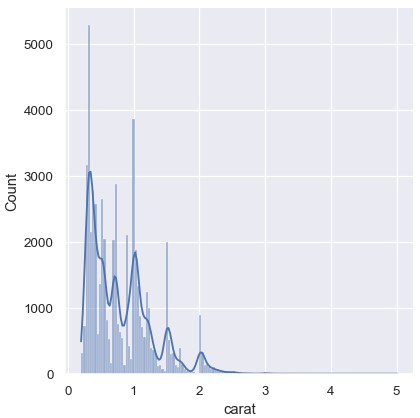
经验累积分布

另一种可视化分布的方法计算的是经验累积分布函数 (ECDF)。这种方法绘制一条经过每个数据点的单调递增的曲线，曲线的高度代表小于该取值的数据所占的比例：

sns.displot(penguins, x='flipper_length_mm', kind='ecdf')

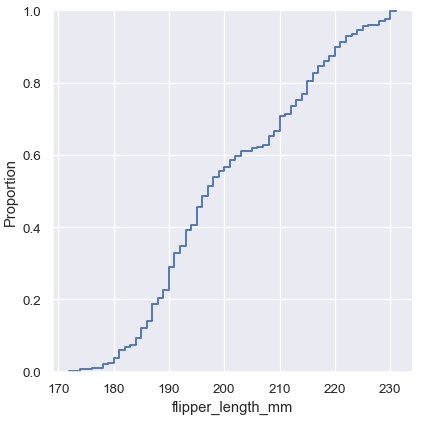
ECDF图有两个关键优势。与直方图或者KDE不同，ECDF直接展示了每个数据点。这意味不需要考虑分箱大小或者平滑参数。另外，由于曲线是单调递增的，也非常适用于多个分布的比较：

sns.displot(penguins, x='flipper_length_mm', hue='species', kind='ecdf')

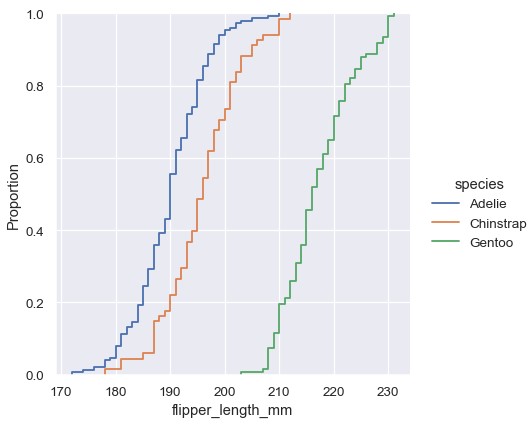
ECDF图的主要缺点是不如直方图或者密度曲线直观。在直方图上能够直接看出鳍状肢长度的双峰分布，而在ECDF图中，需要检查斜率的变化。无论如何，通过实践，你能够学会利用ECDF图回答关于数据分布的各种问题

可视化双变量分布

目前所有的例子都考虑了单变量分布：一个变量的分布情况，以及将另一个变量赋值给hue的情况。如果将另一个变量赋值给y，将绘制出双变量分布：

sns.displot(penguins, x='bill_length_mm', y='bill_depth_mm')

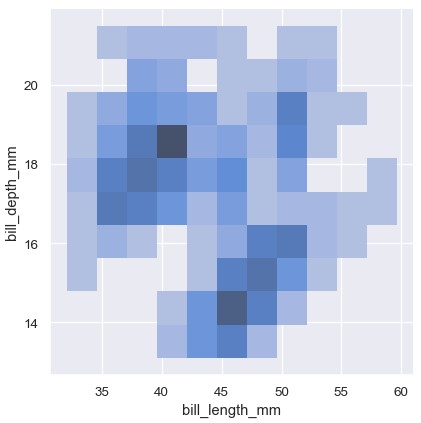
双变量直方图将数据划分到铺满整个图片的正方形中，然后利用每个正方形的颜色展示该正方形内的观测的数量 (与heatmap()类似)。类似的，双变量KDE图使用2D高斯函数对 (x, y)进行平滑处理。绘制默认条件下的2D密度等高线图：

sns.displot(penguins, x='bill_length_mm', y='bill_depth_mm', kind='kde')

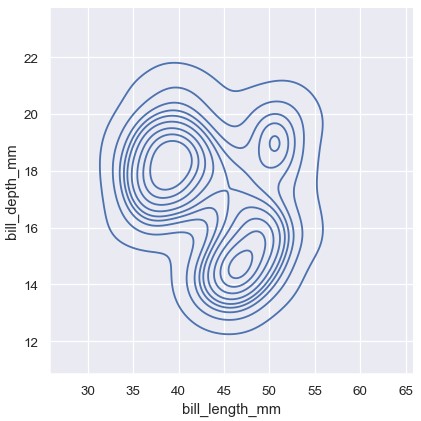
设置hue变量将使用不同颜色绘制多个热图或者等高线图。对于双变量直方图来说，只有在不同颜色的分布重叠很少时效果比较好：

sns.displot(penguins, x='bill_length_mm', y='bill_depth_mm', hue='species')

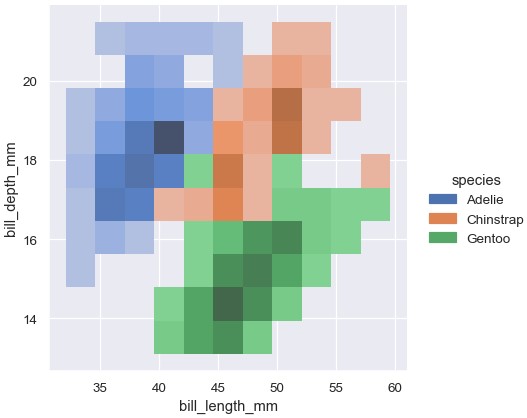
双变量KDE的等高线图能够更好地展示重叠部分，但是在一个图上绘制太多等高线会显得很杂乱：

sns.displot(penguins, x='bill_length_mm', y='bill_depth_mm', hue='species', kind='kde')

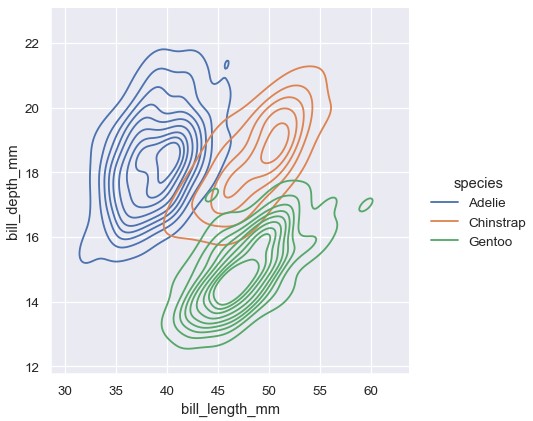
与单变量分布一样，分箱大小和平滑带宽的选择决定了表征双变量分布特征的优劣。同样的参数对于双变量分布也是适用的，但是需要传入一对数值分别调整两个变量：

sns.displot(penguins, x='bill_length_mm', y='bill_depth_mm', binwidth=(2, 0.5))

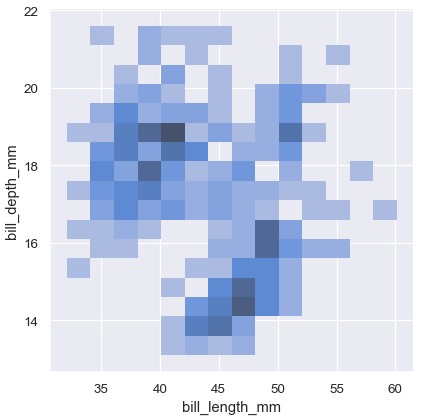
添加色彩条展示计数与颜色之间的映射可以辅助热图的解读：

sns.displot(penguins, x='bill_length_mm', y='bill_depth_mm', binwidth=(2, 0.5), cbar=True)

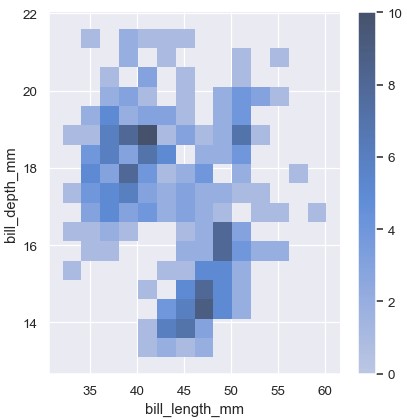
双变量密度等高线图的含义不那么直白。由于密度并不能直接解读，等高线画在密度的相同比例处，意味着每条曲线展示了一组取值，存在一部分密度的比例p低于该取值。p值默认是间隔均匀的，thresh参数控制最低取值，levels参数控制取值的个数：

sns.displot(penguins, x='bill_length_mm', y='bill_depth_mm', kind='kde', thresh=0.2, levels=4)

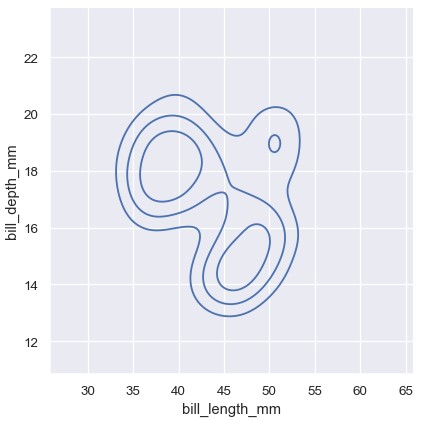
levels参数也可以接受一个列表，精确控制曲线的p值：

sns.displot(penguins, x='bill_length_mm', y='bill_depth_mm', kind='kde', levels=[0.01, 0.05, 0.1, 0.8])

双变量直方图允许一个或者两个变量是离散型。绘制一个离散型一个连续型变量的直方图提供了比较条件单变量分布的另一种方式：

sns.displot(diamonds, x='price', y='clarity', log_scale=(True, False))

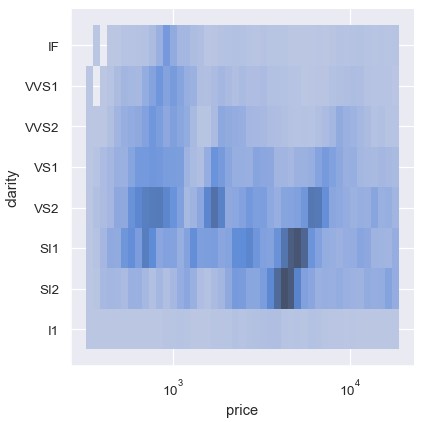
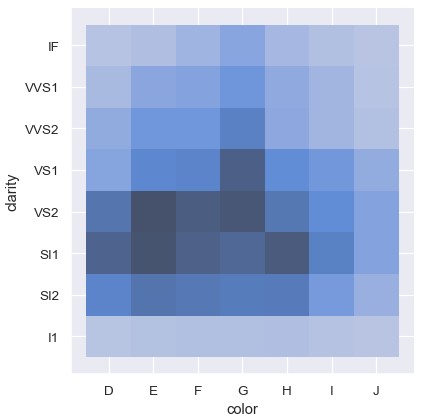
相反，绘制两个连续型变量的直方图提供了一种方便地列联表的方式：

sns.displot(diamonds, x='color', y='clarity')

其它情况下的分布可视化

其它利用了histplot()和kdeplot()的图水平函数

绘制联合及边缘分布

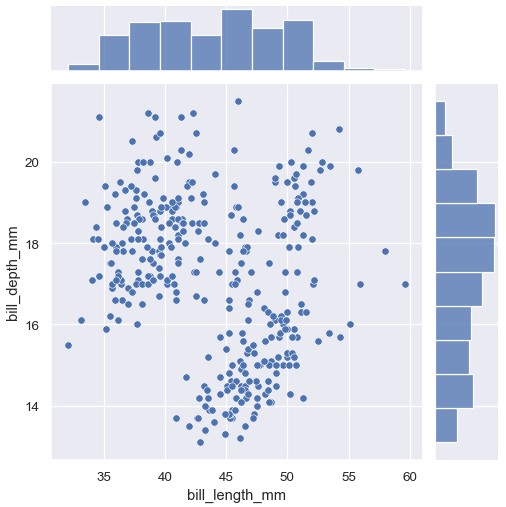
第一个是jointplot()，在双变量关系型或分布图的边缘位置增加了两个变量的分布。在默认情况下，jointplot()使用scatterplot()绘制双变量分布，使用histplot()绘制边缘分布：

sns.jointplot(penguins, x='bill_length_mm', y='bill_depth_mm')

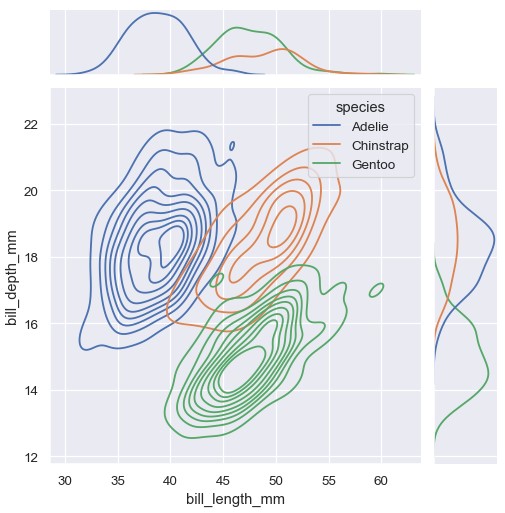
与displot()类似，在jointplot()中设置kind='kde'会使用kdeplot()改变联合及边缘分布的类型：

sns.jointplot(penguins, x='bill_length_mm', y='bill_depth_mm', hue='species', kind='kde')

jointplot()提供了一个JointGrid类的方便接口，从而能够在直接调用时更加灵活：

g = sns.JointGrid(penguins, x='bill_length_mm', y='bill_depth_mm')
g.plot_joint(sns.histplot)
g.plot_marginals(sns.boxplot)

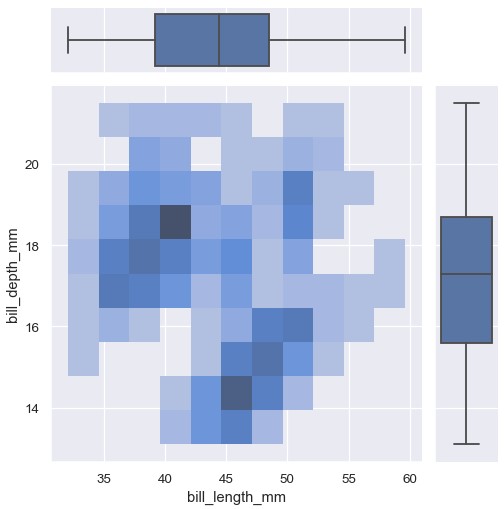
另一种展示边缘分布不那么突兀的方式是地毯图 (rug plot)，通过在图的边缘添加一个小记号体现两个变量独立分布。这种方法也被构建在displot()中：

sns.displot(penguins, x='bill_length_mm', y='bill_depth_mm', kind='kde', rug=True)

轴水平函数rugplot()可以在任意类型的图片边缘添加地毯记号：

sns.relplot(penguins, x='bill_length_mm', y='bill_depth_mm')
sns.rugplot(penguins, x='bill_length_mm', y='bill_depth_mm')

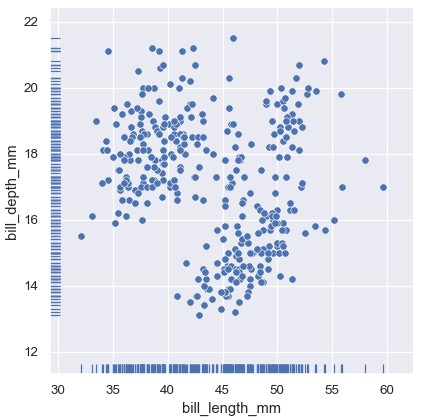
绘制多个分布

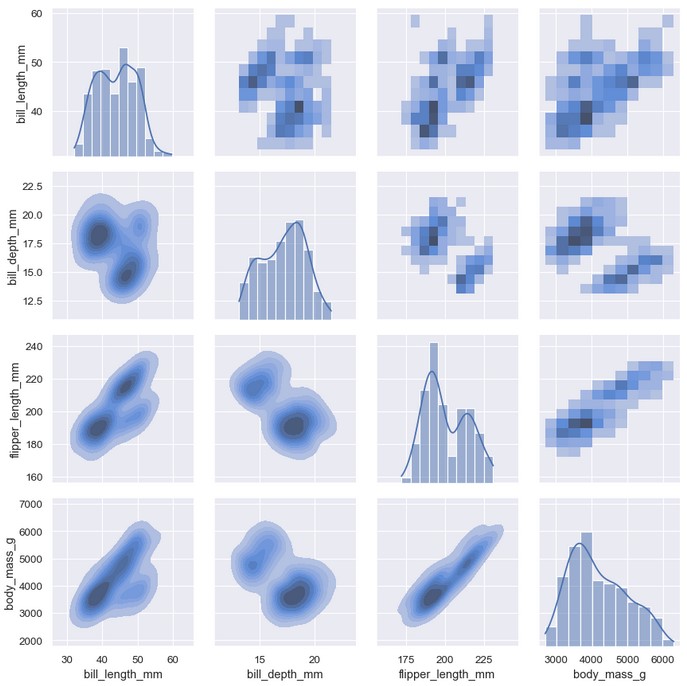
pairplot()函数近似于结合了联合及边缘分布。pairplot()不关注单个相互关系，而是使用小多图的方式，对所有变量的单变量分布和它们两两之间的相互关系同时进行可视化：

sns.pairplot(penguins)

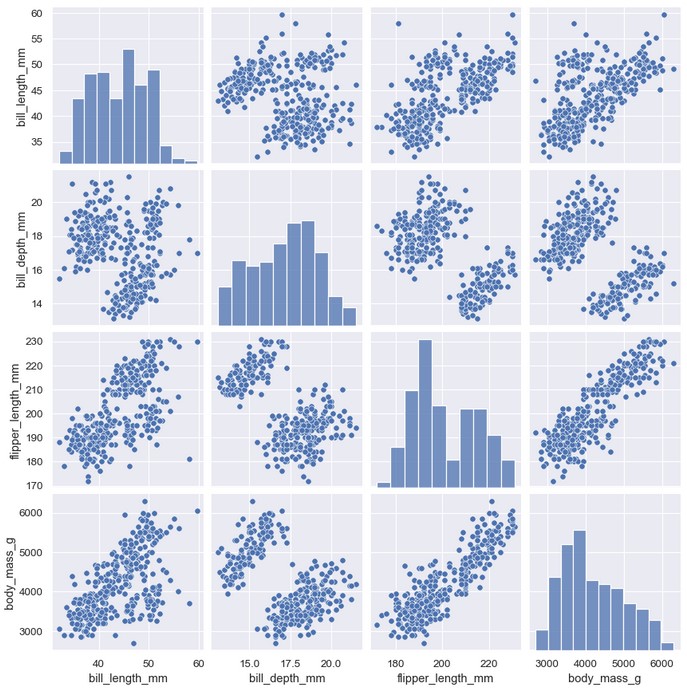
与jointplot() / JointGrid类似，直接调用底层的PairGrid可以在绘图时更加灵活：

g = sns.PairGrid(penguins)
g.map_upper(sns.histplot)
g.map_lower(sns.kdeplot, fill=True)
g.map_diag(sns.histplot, kde=True)