集成学习通过构建并结合多个模型来完成学习任务,通过结合多个模型,实现降低偏差、方差及改进预测结果等目标。为了使得集成学习获得比单一模型更好的泛化性能,我们希望参与集成学习的单一模型好而不同,也就是每个模型必须具备一定的准确性,不同模型之间存在差异(多样性)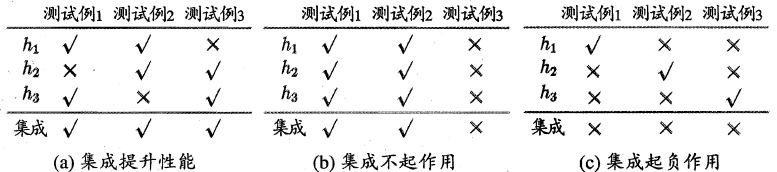
图a的三个模型具备准确性及多样性,集成学习性能提升;图b三个模型具备准确性,缺乏多样性,集成学习不起作用;图c三个模型具备多样性,但准确性差,集成学习性能下降
集成学习的输出策略
Majority voting
- 假设有n个独立的分类模型,每个模型输出一个预测值,取n个预测值的众数作为最终的预测结果:
$$H(x) = c_{\arg \max_j \sum_{i=1}^nh_i^j(x)}$$$h_i^j(x)$ 表示模型 $h_i$ 在类别标记 $c_j$ 上的输出
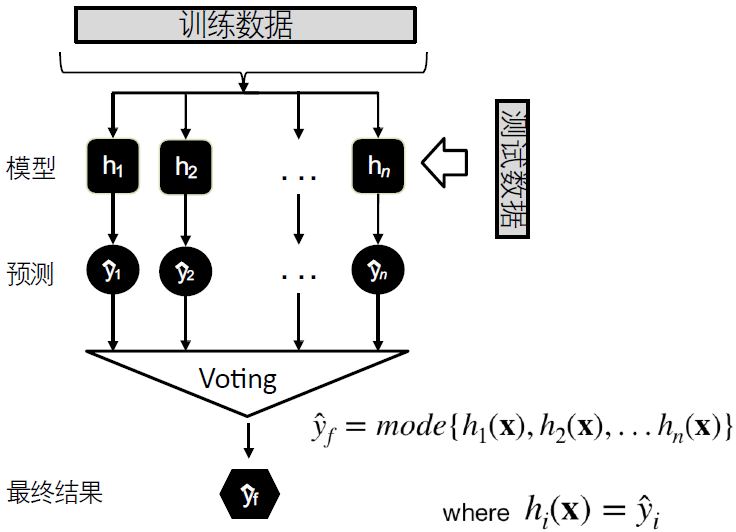
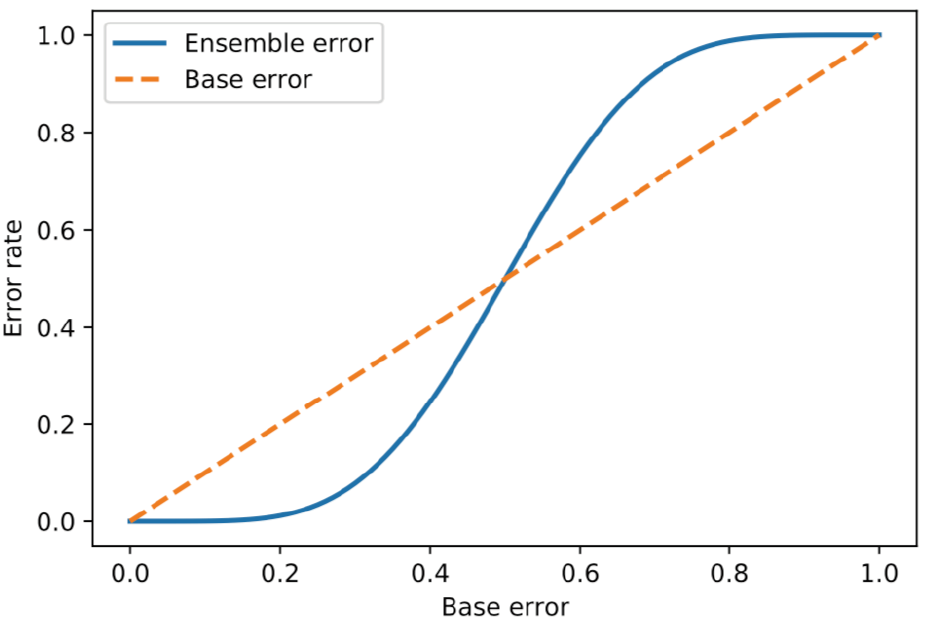
假设这n个独立分类模型为二分类模型,错误率都为 $\epsilon (\epsilon > 0.5)$ ,则有 $k$ 个模型预测错误,并造成最终结果预测错误的概率为:
$$\epsilon_{ens} = \sum_k^n\begin{pmatrix}n \\ k \end{pmatrix}\epsilon^k(1 - \epsilon)^{(n -k)} \quad k > \lceil\frac{n}{2}\rceil$$
当独立模型的错误率低于0.5时,集成学习的错误率总是低于单个独立模型
对于数值型输出的非分类模型,相当于简单平均法,即:
$$H(x) = \frac{1}{n}\sum_{i=1}^nh_i(x)$$
Weighted voting
给每一个独立模型一个权重,在统计投票结果时考虑不同模型的权重:
$$H(x) = c_{\arg \max_j \sum_{i=1}^nw_ih_i^j(x)} \quad s.t. \ w_i \geq 0, \sum_{i=1}^n = 1$$对应于数值型输出模型的加权平均法:
$$H(x) = \sum_{i=1}^nw_ih_i(x) \quad s.t. \ w_i \geq 0, \sum_{i=1}^n = 1$$简单平均法是加权平均法 $w_i = \frac{1}{n}$ 时的特例
单一模型性能差别较大时常使用加权平均法,单一模型性能相近时宜使用简单平均法
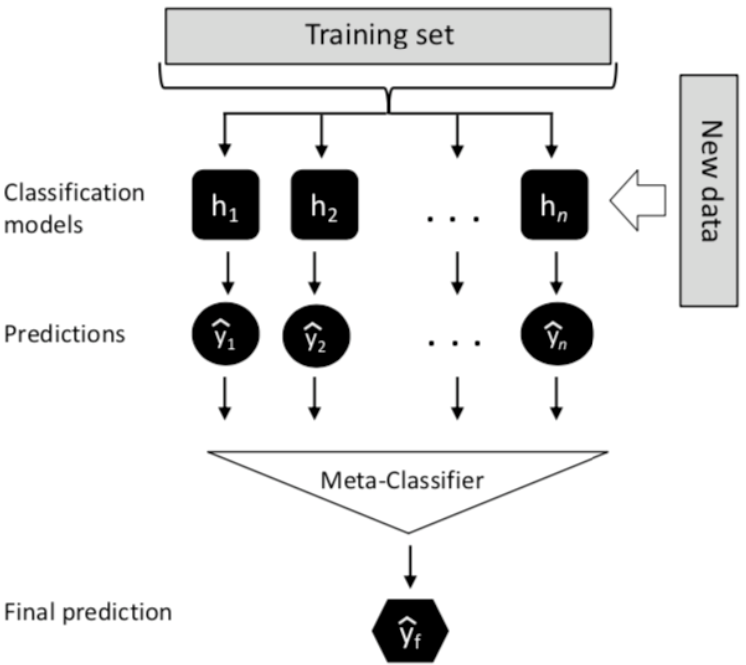
Stacking
先使用初始训练数据训练出一系列初级模型,然后以初级模型的输出作为输入特征,初始训练数据的输出作为标签,训练次级模型

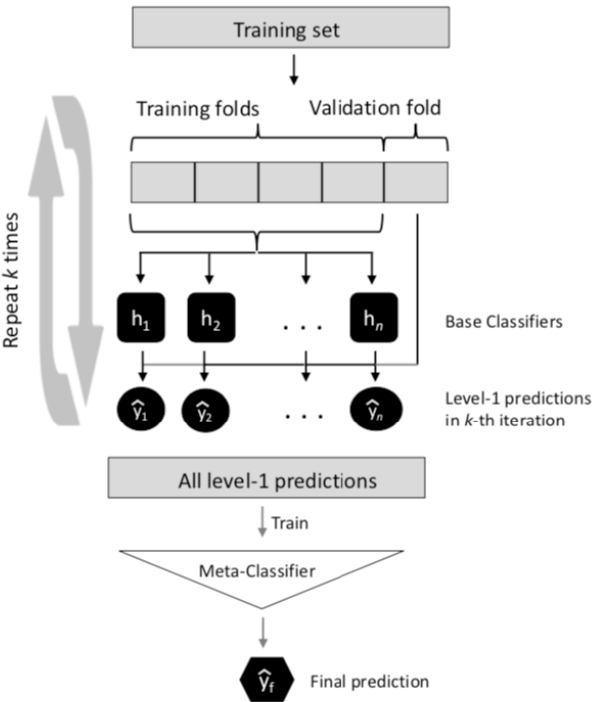
由于次级模型的训练数据是由初级模型产生的,若初级模型已经发生了过拟合,那么次级模型便是基于过拟合的数据继续进行训练,过拟合风险大。为了解决这一问题,通常使用交叉验证法,用初级模型未使用的初始训练数据产生次级模型的训练数据

集成学习方法
目前的集成学习方法大致分为两类:
单个模型之间存在强依赖关系、必须串行生成的序列化方法,如Boosting
单个模型之间不存在强依赖关系、可同时生成的并行化方法,如Bagging和Random forest
Boosting
Boosting致力于降低偏差,能够基于性能较差的模型产生性能较强的集成。首先基于初始训练集训练一个弱的初始模型,然后根据初始模型的表现,为预测错误的训练数据赋予较大的权重,使用带权重的训练数据训练下一个模型,如此循环,直至获得 $n$ 个模型,最终将这个 $n$ 个模型的结果进行加权输出
Boosting算法中最著名的代表是AdaBoost

AdaBoost训练的模型 $H$ 的误差上限为:
$$e^{-2\sum_{t=1}^T\gamma_t^2}; \quad \epsilon_t = \frac{1}{2} - \gamma_t$$
Bagging
Bagging是
Bootstrap Aggregating的缩写,这种算法致力于降低方差自助采样法 (bootstrap sampling):给定包含 $m$ 个样本的数据集,随机去除一个样本放入采样集,然后把该样本放回初始数据集,再进行下一次随机采样,如此重复 $m$ 次,即可获得包含 $m$ 个样本的采样集
包含 $m$ 个样本的数据集中的某条数据,在 $m$ 次采样中都没有被选中的概率是:
$$P(not \ chosen) = (1 - \frac{1}{m})^m$$
当 $m \to \infty$ 时,$P \approx 0.368$ 。即初始训练集中只有 $63.2\%$ 的数据出现在采样集中
对初始训练集进行 $n$ 轮采样,基于每轮获得的采样集训练 $n$ 个模型。对于分类问题一般采取简单投票法输出最终结果,对于回归问题一般采取简单平均法
由于每个采样集只使用了初始训练集中约 $63.2\%$ 的样本,剩下约 $36.8\%$ 的样本可用作验证集来对泛化能力进行袋外估计 (out-of-bag estimate)
Random forest
是Bagging的扩展算法,在以决策树为基础的Bagging集成算法中,进一步引入决策树的随机属性选择
传统决策树是在当前节点的所有 $d$ 个属性中选择一个最优属性进行分枝;随机森林先从该节点的 $d$ 个属性中随机选出一个含有 $k$ 个属性的子集,然后再从这个子集中选择最优属性进行分枝
若 $k = d$ ,相当于传统决策树;若 $k = 1$ ,相当于随机选择一个属性用于分枝
推荐 $k = \log_2 d$