PCA
主成分分析 (principal component analysis, PCA)是一种常用的无监督学习降维方法。其目的是在高维空间中找到一个超平面,使得所有样本点距离这个超平面的距离尽可能近 (最近重构性)且所有样本点在这个超平面上的投影都尽可能分开 (最大可分性)。主成分就是形成这个超平面的正交基向量,将原始数据投影到这个超平面上,即用主成分来表征原始数据,达到降维的目的。
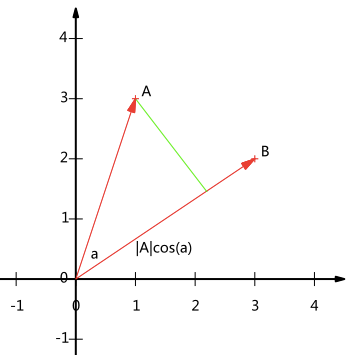
向量内积与投影
假设两个二维向量 $A = (x_1,y_1), \ B = (x_2,y_2)$ ,两个向量的夹角为 $a$ ,则向量 $A$ 在向量 $B$ 方向的投影为 $|A|\cos a$

向量 $A$ 与向量 $B$ 的内积为 $A \cdot B = |A||B|\cos a$ 。若向量 $B$ 的模为1,即 $|B| = 1$ ,则向量 $A$ 在向量 $B$ 方向的投影等于向量 $A$ 与向量 $B$ 的内积
根据向量的模的定义 $|A| = \sqrt{x_1^2 + y_1^2}$ ,对于任何一个向量,只要将其各个分量都除以该向量的模,就得到了与该向量方向相同,且模为1的基向量
对于M个N维向量,若要将其投影到R个N维向量组成的超平面,首先将R个基向量按行排列成左侧矩阵,将M个向量按列排列成右侧矩阵,两个矩阵的乘积就是投影之后的结果
$$\begin{pmatrix}-p_1- \\ -p_2- \\ \vdots \\ -p_R-\end{pmatrix} \begin{pmatrix}| & | & \cdots & | \\a_1 & a_2 & \cdots & a_M \\ | & | & \cdots & |\end{pmatrix} = \begin{pmatrix}p_1a_1 & p_1a_2 & \cdots & p_1a_M \\ p_2a_1 & p_2a_2 & \cdots & p_2a_M \\ \vdots & \vdots & \ddots & \vdots \\ p_Ra_1 & p_Ra_2 & \cdots & p_Ra_M\end{pmatrix}$$左边的矩阵的维度为 $(R,N)$ ,右边矩阵的维度为 $(N,M)$ 相乘后矩阵的维度为 $(R,M)$ 。两个矩阵相乘的物理意义是将右边矩阵中的每一列列向量变换到以左边矩阵中每一行行向量为基的空间中去
方差与协方差
根据最大可分性的目标,我们希望投影后各个样本点尽量分散,这种分散程度可以用方差表示:
$$Var(a) = \frac{1}{m}\sum_{i=1}^m(a_i - \mu)^2; \quad \mu = \frac{1}{m}\sum_{i=1}^m a_i$$为了方便计算,首先将数据进行去中心化,即把每一个元素都减去均值,使得去中心化后的所有元素均值为0,此时方差表示为:
$$Var(a) = \frac{1}{m}\sum_{i=1}^m a_i^2$$对于二维降维成一维的问题,只要找到使方差最大的方向即可。对于更高维的降维问题,在选择其它投影方向时,为了保留更多的原始信息,应该尽可能保证各投影方向之间不存在相关性。用协方差表示向量之间的相关性,若两个向量正交,协方差为0。对于去中心化的向量,其协方差为:
$$Cov(a,b) = \frac{1}{m}\sum_{i=1}^m a_ib_i$$矩阵 $X$ 的协方差矩阵可表示为:
$$C = \frac{1}{m}XX^T$$
PCA优化目标
假设我们找到一个单位基向量 $u_1$ ,将去中心化的 $x_i$ 在 $u_1$ 方向上进行投影,则投影后的向量为 $u_1^Tx_i$
投影后的向量均值为:
$$\frac{1}{m}\sum_{i=1}^m u_1^Tx_i = u_1^T\frac{1}{m}\sum_{i=1}^m x_i = 0$$投影后的方差为:
$$\begin{align}
\frac{1}{m}\sum_{i=1}^m (u_1^Tx_i)^2 & = \frac{1}{m}\sum_{i=1}^m u_1^Tx_ix_i^Tu_1 \\
& = u_1^T\frac{1}{m}\sum_{i=1}^m x_ix_i^Tu_1 \\
& = u_1^T C u_1 \\
C = \frac{1}{m}XX^T
\end{align}$$PCA的优化目标为:
$$\max_{u_1} \ u_1^T C u_1 \qquad s.t. ||u_1||_2^2 = 1$$将目标函数添加拉格朗日算子:
$$L = u_1^TCu_1 + \lambda(1 - ||u_1||^2_2)$$对 $u_1$ 求导,令导数为0:
$$\begin{align}
& \frac{\partial L}{\partial u_1} = 2u_1 C + \lambda (-2u_1) = 0 \\
& \implies Cu_1 = \lambda u_1
\end{align}$$$\lambda$ 和 $u_1$ 分别为协方差矩阵 $C$ 的特征值和特征向量
推广到多维超平面可得,目标函数 $U^TCU = U\lambda U$ 。由于 $U$ 由一系列单位基向量组成, $U^TU = 1$ , $U^TCU = U^T\lambda U = \lambda$ 。协方差矩阵的特征值等于矩阵 $X$ 投影后的方差,要想最大化方差,投影方向应该选择协方差矩阵最大特征值对应的特征向量
将协方差矩阵的特征值由大到小排列,提取对应的前K行特征向量组成矩阵 $(u_1,u_2,\cdots,u_k)$ 乘以去中心化的矩阵 $X$ ,就得到了降维后的矩阵
PCA算法总结
对于m条包含n个特征的数据:
将数据按列组成n行m列的原始矩阵
将原始矩阵中的每个元素减去所在行各元素的均值,得到去中心化的矩阵 $X$
求出协方差矩阵 $C = \frac{1}{m}XX^T$
求出协方差矩阵的特征值及对应的特征向量
将特征值由大到小排列,提取对应的前K行特征向量组成矩阵 $P$
$Y = PX$ 即为降到K维后的数据
LDA
线性判别分析 (linear discriminant analysis, LDA)是一种监督学习的算法。其核心思想是将高维的数据投影到一条直线上,是的同类别的数据投影点尽可能接近,不同类别的数据投影点尽可能远离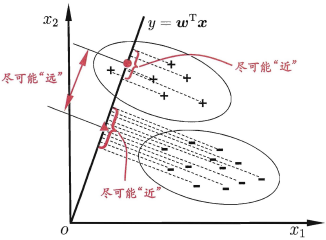
LDA算法推导
以二分类为例,假设有样本 $C_1, C_2$ ,其均值分别为 $\mu_1, \mu_2$ ,投影方向为 $w$ 。则投影后两个样本之间的距离为:
$$D(C_1, C_2) = ||w^T(\mu_1 - \mu_2)||^2_2$$投影后两个样本的方差分别为:
$$\begin{align}
& Var(C_1^{\prime}) = \sum_{x \in C_1}(w^Tx - w^T\mu_1)^2 \\
& Var(C_2^{\prime}) = \sum_{x \in C_2}(w^Tx - w^T\mu_2)^2
\end{align}$$根据最大化类间距离和最小化类内距离的目标,可以将目标函数表示为:
$$\begin{align}
\max_w J(w) & = \frac{D(C_1, C_2)}{Var(C_1^{\prime}) + Var(C_2^{\prime})} \\
& = \frac{w^T(\mu_1 - \mu_2)(\mu_1 - \mu_2)^Tw}{\sum_{x \in C_i}w^T(x - \mu_i)(x - \mu_i)^Tw}
\end{align}$$定义类内散度矩阵 $S_w$ :
$$S_w = \sum_{x \in C_i}(x - \mu_i)(x - \mu_i)^T$$定义类间散度矩阵 $S_b$ :
$$S_b = (\mu_1 - \mu_2)(\mu_1 - \mu_2)^T$$将目标函数简化为:
$$J(w) = \frac{w^TS_bw}{w^TS_ww}$$对 $J(w)$ 求 $w$ 的偏导数,令导数为0:
$$\begin{align}
\frac{\partial J}{\partial w} & = 2S_bw(w^Ts_ww)^{-1} - 2S_ww(w^TS_bw)(w^TS_ww)^{-2} \\
& = 2S_bw - 2S_ww(w^TS_bw)(w^TS_ww)^{-1} = 0 \\
& \implies (w^TS_ww)S_bw = (w^TS_bw)S_ww \\
& \implies \frac{w^TS_bw}{w^TS_ww} = \frac{S_bw}{S_ww}
\end{align}$$将上式带回目标函数可得:
$$\begin{align}
& J(w) = \frac{Sbw}{S_ww} \\
& S_bw = J(w)S_ww \\
& S_w^{-1}S_bw = J(w)w
\end{align}$$$J(w)$ 和 $w$ 分别对应了矩阵 $S_w^{-1}S_b$ 的特征值和特征向量,要想最大化目标函数,只需要求得矩阵 $S_w^{-1}S_b$ 的最大特征向量,投影方向为该特征值对应的特征向量
扩展到多类高维,定义全局散度矩阵 $S_t$ :
$$S_t = S_b + S_w = \sum_{i=1}^m(x_i - \mu)(x_i - \mu)^T$$$\mu$ 为全局中心, $N$ 为类别数, $m$ 为样本数
此时,类内散度矩阵定义为每个类的类内散度矩阵之和:
$$S_w = \sum_{i=1}^NS_{wi}$$可以推导出类间散度矩阵的定义:
$$S_b = \sum_{i=1}^Nm_i(\mu_i - \mu)(\mu_i - \mu)^T$$
LDA算法总结
计算每个类别的均值 $\mu_i$ 和全局中心 $\mu$
计算全局散度矩阵 $S_t$ ,类内散度矩阵 $S_w$ 和类间散度矩阵 $S_b$
求矩阵 $S_w^{-1}S_b$ 的特征值和特征向量
将矩阵 $S_w^{-1}S_b$ 的特征值从大到小排列,取前K个特征值对应的特征向量
计算投影矩阵