从线性回归到逻辑回归
线性回归模型假设输入样本矩阵 $X$ 与输出特征向量 $y$ 之间满足 $y = X\theta$ 的线性关系,输出的 $y$ 是连续的,因此是一个回归模型。而逻辑回归虽然名为回归,实际上是一个分类模型。逻辑回归相当于将线性回归模型输出的 $y$ 再进行一次函数转换,得到 $g(y)$ 。虽然线性回归模型不能拟合离散变量,但可以拟合预测为某一类别的概率,即 $P(y = 1|x) = g(y)$。定义一个阶跃函数,使得当 $g(y) > 0.5$ 时输出 $1$ ,其余情况输出 $0$ ,这样就得到了一个二元分类模型。但是,阶跃函数是不可微的,给模型优化造成一定困难,因此使用Sigmoid函数代替这个阶跃函数,就得到了逻辑回归模型。
Sigmoid函数
$$g(z) = \frac{1}{1 + e^{-z}}$$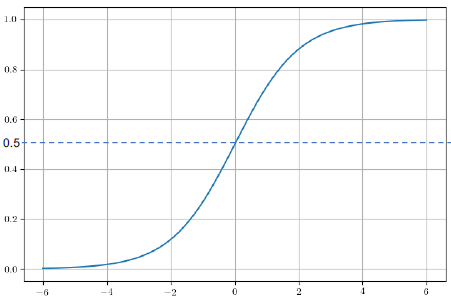
当 $z$ 趋近于 $\infty$ 时, $g(z)$ 趋近于 $1$ ;当 $z$ 趋近于 $-\infty$ 时, $g(z)$ 趋近于 $0$
$g^{\prime}(z) = g(z)(1 - g(z))$
令 $z = X\theta$ ,则逻辑回归模型的一般形式为:
$$\begin{align}
h_{\theta}(x) & = \frac{1}{1 + e^{-z}} \\
& = \frac{1}{1 + e^{-X\theta}}
\end{align}$$
逻辑回归的损失函数
$$J(\theta) = -\frac{1}{m}\sum_{i=1}^m[y_i\ln h_{\theta}(x_i) + (1 - y_i)\ln (1 - h_{\theta}(x_i))]$$
最大似然估计
逻辑回归的损失函数可以通过极大似然估计 (maximum likelihood estimation, MLE)进行推导:
样本分类为 $1$ 或 $0$ 的概率为:
$$\begin{align}
& P(y = 1|x,\theta) = h_{\theta}(x) \\
& P(y = 0|x,\theta) = 1 - h_{\theta}(x)
\end{align}$$将两个式子合并:
$$P(y|x,\theta) = h_{\theta}(x)^y(1 - h_{\theta}(x))^{1 - y} \qquad y \in \lbrace0, 1\rbrace$$似然函数:
$$L(\theta) = \prod_{i=1}^mh_{\theta}(x_i)^{y_i}(1 - h_{\theta}(x_i))^{1 - y_i}$$将似然函数两边取对数,再加负号求均值,即得到损失函数:
$$\begin{align}
J(\theta) & = -\frac{1}{m}\ln L(\theta) \\
& = -\frac{1}{m}\sum_{i=1}^m [y_i\ln h_{\theta}(x_i) + (1 - y_i)\ln (1 - h_{\theta}(x_i))]
\end{align}$$
逻辑回归的损失函数是凸函数
证明一个函数是凸函数的思路:
- $f(\alpha x + (1 - \alpha)y) \leq f(\alpha x) + f((1 - \alpha)y)$
- $f(x + \epsilon) \geq f(x) + \nabla f(x)\epsilon$
- $f(x)$ 的Hessian矩阵 ${\nabla}^2f(x)$ 是半正定的
$$\begin{align}
& J(\theta) = \frac{1}{m}[\sum_{i=1}^m y_i(-\ln h_{\theta}(x_i)) + \sum_{i=1}^m (1 - y_i)(-\ln (1 - h_{\theta}(x_i))] \\
& \text{其中:} \quad h_{\theta}(x_i) = \frac{1}{1 + e^{-\theta^Tx_i}}
\end{align}$$
先证明 $-\ln h_{\theta}(x) = -\ln \frac{1}{1 + e^{-\theta^Tx}} = \ln (1 + e^{-\theta^Tx})$ 的Hessian矩阵半正定
对 $-\ln h_\theta(x)$ 求梯度:
$$\begin{align}
\nabla_\theta (-\ln h_\theta(x)) & = \nabla_{\theta}[\ln (1 + e^{-\theta^Tx})] \\
& = \frac{0 - e^{-\theta^Tx}}{1 + e^{-\theta^Tx}}x \\
& = (\frac{1}{1 + e^{-\theta^Tx}} - 1)x \\
& = (h_{\theta}(x) - 1)x
\end{align}$$$-\ln h_\theta(x)$ 的Hessian矩阵:
$$\begin{align}
\nabla^2_{\theta}(-\ln h_\theta(x)) & = \nabla_\theta[(h_\theta(x) - 1)x] \\
& = h_\theta(x)[1 - h_\theta(x)]xx^T
\end{align}$$$-\ln h_\theta(x)$ 的Hessian矩阵是半正定的:
$$\begin{align}
\forall z: \ z^T\nabla^2_\theta(-\ln h_\theta(x))z & = z^Th_\theta(x)[1 - h_\theta(x)]xx^Tz \\
& = h_\theta(x)[1 - h_\theta(x)]z^Txx^Tz \\
& = h_\theta(x)[1 - h_\theta(x)] (x^Tz)^2 \geq 0
\end{align}$$同理可证, $-\ln (1 - h_\theta(x))$ 的Hessian矩阵是半正定的
$-\ln h_\theta(x)$ 和 $-\ln (1 - h_\theta(x))$ 的Hessian矩阵都是半正定的,则它们的线性组合也是半正定的
为什么不用最小二乘估计
若使用最小二乘估计 (MSE),则损失函数为:
$$L_{MSE} = \frac{(y - y_{pred})^2}{2}$$将 $L_{MSE}$ 对参数 $\theta$ 求导:
$$\frac{\partial L_{MSE}}{\partial \theta} = (y - y_{pred})g^{\prime}(\theta^Tx)x$$由于 $g^{\prime}(z) = g(z)(1 - g(z))$ ,且当 $z \to \infty$ 时, $g(z) \to 1$ ,此时 $1 - g(z) \to 0$ ;而当$z \to -\infty$ 时, $g(z) \to 0$ 。
也就是说,当 $\theta^Tx$ 特别大或特别小时,使用最小二乘估计的梯度都会非常小,导致收敛变慢,甚至在训练过程中可能因为梯度过小而提前终止训练 (梯度消失)
使用最大似然估计时,损失函数为:
$$L_{MLE} = -y\ln y_{pred} - (1 - y)(1 - \ln (1 - y_{pred}))$$将 $L_{MLE}$ 对参数 $\theta$ 求导:
$$\begin{align}
\frac{\partial L_{MLE}}{\partial \theta} & = -y\frac{1}{g(\theta^Tx)}g(\theta^Tx)(1 - g(\theta^Tx))x + (1 - y)\frac{1}{1 - g(\theta^Tx)}g(\theta^Tx)(1 - g(\theta^Tx))x \\
& = x(g(\theta^Tx) - y)
\end{align}$$当模型输出与实际概率有较大差别时, $g(\theta^Tx) - y$ 比较大,梯度较大,训练速度较快;当模型输出接近真实概率时,训练速度放缓
扩展到多元分类
假设是K元分类模型,则模型输出取值为1,2…,K:
$$\begin{align}
h_\theta(x) & = \begin{bmatrix}P(y=1|x,\theta) \\ P(y=2|x,\theta) \\
\vdots \\ P(y=K|x,\theta)\end{bmatrix} \\
& = \frac{1}{\sum_{i=1}^Ke^{\theta_i^Tx}}\begin{bmatrix}e^{\theta_1^Tx} \\ e^{\theta_2^Tx} \\ \vdots \\ e^{\theta_K^Tx}\end{bmatrix}
\end{align}$$
$$\theta = \begin{bmatrix}| & | & | & | \\ \theta_1 & \theta_2 & \cdots & \theta_K \\ | & | & | & |\end{bmatrix}$$


