线性回归

线性回归

基本形式

线性回归是一个通过特征的线性组合来进行预测的模型，其基本形式为：
$$f(x) = w_1x_1 + w_2x_2 + … + w_nx_n + b$$
写成向量的形式即为：
$$f(x) = w^Tx + b$$
由于 $w$ 直观表达了各属性在预测中的重要性，因此，线性模型具有很好的可解释性 (comprehensibility)

为了表示方便，将所有 $x_i$ 组合成一个矩阵，并额外添加一个值全为 $1$ 的列，将 $b$ 吸收进 $w$ 中，即：
$$\begin{align}
& X = \begin{pmatrix} x_{11} & x_{12} & … & x_{1n} & 1 \\ x_{21} & x_{22} & … & x_{2n} & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\
x_{m1} & x_{m2} & … & x_{mn} & 1\end{pmatrix} \\
& w = (w_{old}, \ b) \\
& f(x) = Xw
\end{align}$$

其中，样本数为 $m$ ，特征数为 $n$ ；$X$ 的维度为 $(m, n+1)$ ，$Y$ 的维度为 $(m, 1)$ $w$ 的维度为 $(n+1, 1)$

优化目标

在回归问题中，常使用均方误差 (square loss)衡量预测值与实际值之间的差别，即：
$$err(f(x_i),y_i) = (f(x_i) - y_i)^2$$
均方误差有很好的几何意义，它对应了常用的欧几里得距离 (Euclidean distance)。基于最小化均方误差求解模型的方法称为最小二乘法 (least square method)

线性回归的优化目标为：
$$\arg \min_w \sum_{i=1}^m(f(x_i) - y_i)^2 = \ \arg \min_w \sum_{i=1}^m (w^Tx_i - y_i)^2$$

求解 $w$ 的过程称为线性回归模型的最小二乘参数估计 (parameter estimation)

为方便求导，将线性回归的损失函数写为：
$$J(w) = \frac{1}{2m} \sum_{i=1}^m (w^Tx_i - y_i)^2$$

解析解

• 均方误差可以表示为：
  $$\begin{align}
  L(w) & = ||Xw - Y||^2 \\
  & = (Xw - Y)^T(Xw - Y) \\
  & = Y^TY - Y^TXw - w^TX^TY + w^TX^TXw
  \end{align}$$

• 对 $w$ 求导可得：
  $$\begin{align}
  \frac{\partial{L}}{\partial{w}} & = 0 - X^TY - X^TY + 2X^TXw \\
  & = 2X^TXw - 2X^TY
  \end{align}$$

• 令 $\frac{\partial{L}}{\partial{w}} = 0$ 可得：
  $$X^TXw = X^TY \implies w = (X^TX)^{-1}X^TY$$

  通常情况下， $特征数 \ n << 样本数 \ m$ ，使得 $X^TX$ 满秩，有唯一解。若 $样本数 \ m < 特征数 \ n$ ，则可解出多个 $w$ ，都能使得均方误差最小。

• 实际求解过程中，一般会直接计算 $(X^TX)^{-1}X^T$， 该式称为 $X$ 的伪逆

多项式回归

• 当训练数据的分布不符合线性模型时，可以将每一个特征的幂次方添加为一个新的特征对训练数据进行拓展，然后在这个经过拓展的数据集上进行线性拟合，称为多项式回归

• 示例：

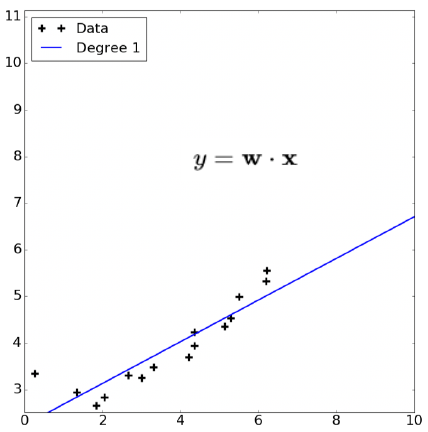
  1. 对数据 $x$ 进行线性拟合，如图所示
     

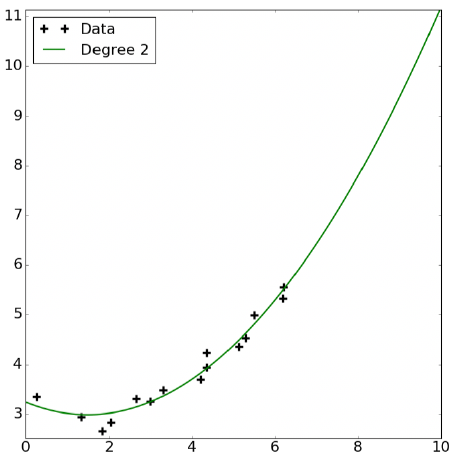
  2. 令 $\phi(x) = [1,x,x^2]$ ，对 $\phi(x)$ 进行线性拟合，即 $y = w_0 + w_1x + w_2 x^2 = \phi(x) \cdot [w_0,w_1,w_2]$ ,如图所示
     

• 对原训练集进行的扩展并非幂次越高越好，幂次方过高容易造成过拟合

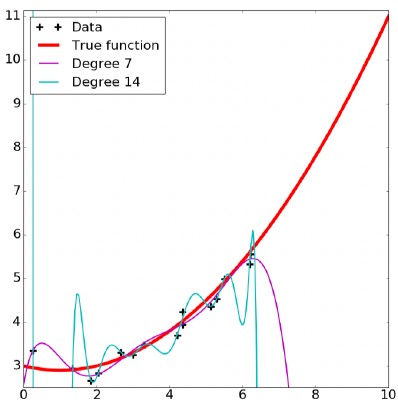
过拟合与欠拟合

偏差和方差

在训练模型的过程中存在两种误差，分别是偏差和方差。偏差表示预测值与实际值之间的差异，方差表示模型对数据变化的敏感程度

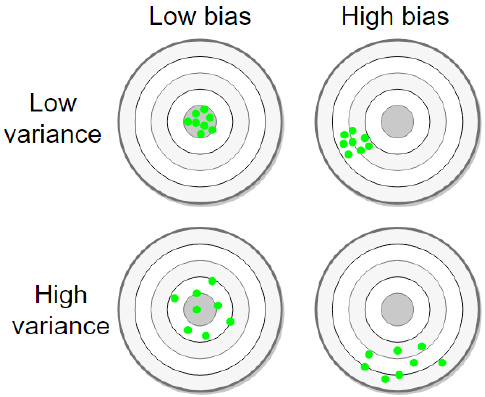
左上图训练数据的分布比较集中，且与圆心的预测值较好地吻合，此时方差和偏差都比较小；右上图数据的分布比较集中，但与预测值相互偏离，此时方差较小，但偏差较大；左下图训练数据分布在预测值附近，但其分布较为分散，此时偏差较小，但方差较大；右下图数据分布较为分散，且偏离预测值，此时方差和偏差都比较大

• 造成高偏差的根本原因是模型太简单，不能很好地拟合训练数据，导致预测值与真实值差别较大，这种情况就是欠拟合

• 造成高方差的原因往往是模型过于复杂，对训练数据过于依赖，极小的数据扰动就会造成预测结果的巨大变化，这种情况就是过拟合

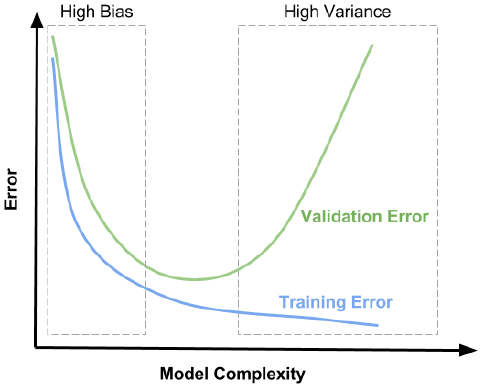
机器学习的很多算法本质上就是高方差的算法，例如KNN、决策树等非参数学习的算法；而线性回归、神经网络等参数学习的算法通常是高偏差的算法。模型调参的过程本质上是权衡方差和偏差的过程，一般而言，降低方差的同时，模型的偏差会增大；而降低偏差的同时，模型的方差会增大

• 欠拟合的解决方法

  1. 增加特征的数量
  2. 增加模型复杂度

• 过拟合的解决方法

  1. 增加训练数据
  2. 降低模型复杂度
  3. 对特征进行筛选
  4. 正则化

正则化

通过在损失函数中添加正则化项，对模型中权重较大的特征进行惩罚，从而避免模型对某些特征过度依赖，降低模型的复杂度

L1正则 (Lasso回归)

$$J(\theta) = \frac{1}{2m}\sum_{i=1}^m(w^Tx_i - y_i)^2 + \lambda||w||_1$$

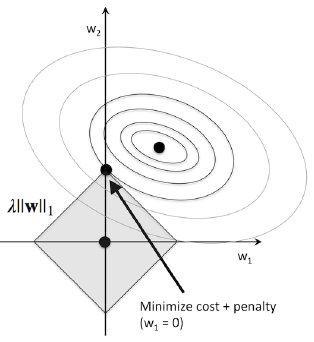
将原始的损失函数记为 $J_0$ ，经过L1正则化的损失函数记为 $J = J_0 + L1$ ，其中 $L1 = \lambda||w||_1$ 。在二维情况下， $J_0$ 对应的等高线如图中同心圆环， $L1$ 对应的等高线如图中正方形所示。在位于正方形顶点的位置可以取得 $J$ 的最小值，而在顶点处意味着和某些坐标轴相交，即某些 $w_i$ 的值为0

• 不易计算，在顶点处连续但不可导

• 通过L1正则化，可以将某些特征的权重缩小到零，从而起到特征筛选的作用

• 由于可以执行隐式的特征筛选，因此通常是特征数量巨大时的首选方案

• 与L2正则化相比通常效果较差

• 对异常值具有更好的抵抗力

L2正则 (Ridge回归)

$$J(\theta) = \frac{1}{2m}(w^Tx_i - y_i)^2 + \lambda||w||_2^2$$

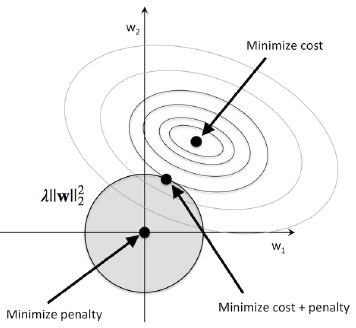
将原始的损失函数记为 $J_0$ ，经过L2正则化的损失函数记为 $J = J_0 + L2$ ，其中 $L2 = \lambda||w||_2^2$ 。在二维情况下， $J_0$ 对应的等高线如图中同心椭圆环， $L2$ 对应的等高线如图中正圆形所示。在 $J_0$ 与 $L2$ 相切的位置可以取得 $J$ 的最小值

• 容易计算，可导，梯度下降法适用

• 将一些特征的权重缩小到接近零但不为零

• 当特征数量巨大时，计算量比较大

• 对异常值非常敏感

ElasticNet

$$J(\theta) = \frac{1}{2m}(w^Tx_i - y_i)^2 + \lambda(\gamma||w||_1 + \frac{1 - \gamma}{2}||w||_2^2)$$

是L1正则和L2正则的凸组合，其中 $\gamma$ 控制L1正则与L2正则的强度