线性规划 (linear programming)
定义
在数学中,线性规划特指目标函数和约束条件皆为线性函数的最优化问题
可行解:满足线性约束条件的解
可行域:由所有可行解组成的集合
最优解:使目标函数取得极值的可行解
举个例子
$$\begin{align}
& max \ \ x_1 + x_2 \\
s.t. \ & 4x_1 - x_2 \leq 8 \\
& 2x_1 + x_2 \leq 10 \\
& 5x_1 - 2x_2 \geq -2 \\
& x_1, \ x_2 \geq 0
\end{align}$$
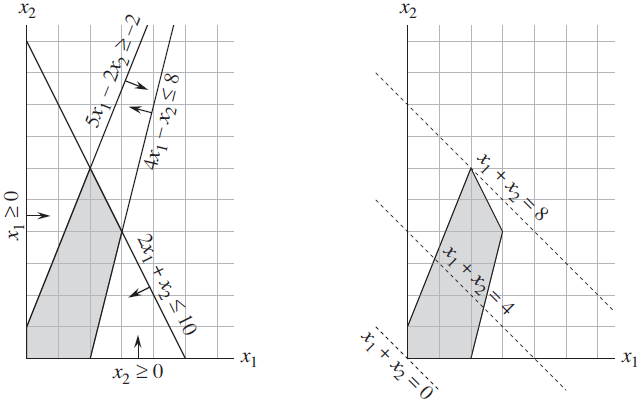
左图中的三条实线加上两个坐标轴即为线性约束条件,由线性约束条件围成的灰色的凸集即为可行域,可行域中的每个点都是可行解。右图中的三条虚线表示去不同可行解时,被优化的目标函数取得不同的值。不难看出,当 $x_1 = 2, \ x_2 = 6$ 时,目标函数取得极大值8,该可行解为最优解
线性规划标准形式
$$\begin{align}
& min \ \ c^Tx \\
s.t. \ & Ax \leq b \\
& x \geq 0
\end{align}$$
格式要求
优化目标为求极小值的形式
线性不等式约束为 $\leq$ 的形式
所有变量都是非负的
标准形式的转换
加负号将求极大值的问题转化成求极小值的问题,或将 $\geq$ 的约束转化为 $\leq$ 的约束
非负变量 $x_i$ 用 $x_i^{\prime} - x_i^{\prime \prime}$ 代替,并添加非负性约束 $x_i^{\prime} \geq 0, \ x_i^{\prime \prime} \geq 0$
等式约束转换为 $\geq$ 和 $\leq$ 的约束,并进一步将 $\geq$ 转化为 $\leq$ 约束
线性规划松弛形式
为了更高效地求解线性规划问题,引入松弛变量,将不等式约束转换为等式约束,即:
$$\begin{align}
& min \ \ c^Tx \\
s.t. \ & Ax = b \\
& x \geq 0
\end{align}$$
- 例子:
$$\begin{align}
& max \ \ x_1 + x_2 \implies min \ \ -x_1 - x_2 \\
s.t. \ & 4x_1 - x_2 \leq 8 \implies 4x_1 - x_2 + x_3 = 8 \\
& 2x_1 + x_2 \leq 10 \implies 2x_1 + x_2 + x_4 = 10 \\
& 5x_1 - 2x_2 \geq -2 \implies -5x_1 + 2x_2 + x_5 = 2 \\
& x_1, \ x_2 \geq 0 \implies x_1, \ x_2, \ x_3, \ x_4, \ x_5 \geq 0
\end{align}$$
最优解一定在可行域的顶点上
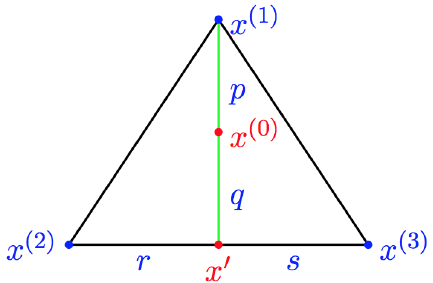
假定 $x^{(0)}$ 是一个可行解;
连接 $x^{(1)}$ 和 $x^{(0)}$ ,延长至与 $x^{(2)}$ 和 $x^{(3)}$ 之间的连线相交,交点为 $x^{\prime}$;
$x^{(0)} = \lambda_1 x^{(0)} + (1 - \lambda_1)x^{\prime}$ ,其中 $\lambda_1 = \frac{q}{p + q}$;
$x^{\prime} = \lambda_2 x^{(2)} + (1 - \lambda_2)x^{(3)}$ ,其中 $\lambda_2 = \frac{s}{r + s}$;
将两式合并可得 $x^{(0)} = \lambda_1 x^{(1)} + (1 - \lambda_1)\lambda_2x^{(2)} + (1 - \lambda_2)x^{(3)}$ ,且 $\lambda_1 + (1 - \lambda_1)\lambda_2 + (1 - \lambda_1)(1 - \lambda_2) = 1$;
假定 $c^Tx^{(1)}$ 是 $c^Tx^{(1)}$ , $c^Tx^{(2)}$ , $c^Tx^{(3)}$ 中的最小值,那么:
$$\begin{align}
c^Tx^{(0)} & = \lambda_1c^Tx^{(1)} + (1 - \lambda_1)\lambda_2c^Tx^{(2)} + (1 - \lambda_1)(1 - \lambda_2)c^Tx^{(3)} \\
& \geq \lambda_1c^Tx^{(1)} + (1 - \lambda_1)c^Tx^{(1)} + (1 - \lambda_1)(1 - \lambda_2)c^Tx^{(1)} \\
& = c^Tx^{(1)}
\end{align}$$
即 $c^Tx^{(1)} \leq c^Tx^{(0)}$ ,位于顶点上的 $x^{(1)}$ 并不比 $x^{(0)}$ 差
单纯形算法 (simplex)
实现步骤:
- 将线性规划的目标函数转换成标准形式
- 将标准形式线性规划转换成松弛形式
- 找到一个初始的基本可行解
- 寻找替入变量和替出变量,替换目标函数,不断地进行旋转 (pivot)
- 重复旋转直至目标函数中没有系数为负的项,算法收敛
几何理解:通过旋转,将当前的可行解从一个顶点移动到另一个顶点,直至求得最优解
示例
优化问题:
$$\begin{align}
& min \ \ -x_1 - x_2 \\
s.t. \ & 4x_1 - x_2 + x_3 = 8 \\
& 2x_1 + x_2 + x_4 = 10 \\
& -5x_1 + 2x_2 + x_5 = 2 \\
& x_1, \ x_2, \ x_3, \ x_4, \ x_5 \geq 0
\end{align}$$将松弛变量单独放在等式约束的左边:
$$\begin{align}
& min \ \ -x_1 - x_2 \\
s.t. \ & x_3 = 8 - 4x_1 + x_2 \\
& x_4 = 10 - 2x_1 - x_2 \\
& x_5 = 2 + 5x_1 - 2x_2 \\
& x_1, \ x_2, \ x_3, \ x_4, \ x_5 \geq 0
\end{align}$$等式约束左边的 ($x_3, x_4, x_5$) 称为基本变量,右边的 ($x_1, x_2$) 称为非基本变量
令 $x_1 = 0, x_2 = 0$ ,此时 $x_3 = 8, x_4 = 10, x_5 = 2$ ,作为基本可行解,目标函数的值为0
第一次旋转
目标函数中系数为负数的非基本变量为替入变量,约束条件中对替入变量约束最严格的基本变量为替出变量
替入变量为 $x_1$
分别计算在 $x_1$ 在3个条件中的约束值:
- $x_1 = 0$
- $x_1 = 5$
- $x_1 = \infty$
当前替出变量为 $x_3$ , $x_1 = \frac{8 + x_2 - x_3}{4}$
第一次旋转后:
$$\begin{align}
& min \ \ \frac{x_3 - 5x_2 - 8}{4} \\
s.t. \ & x_1 = \frac{8 + x_2 - x_3}{4} \\
& x_4 = 6 - 1.5x_2 + 0.5x_3 \\
& x_5 = 12 -0.75x_2 - 1.25x_3 \\
& x_1, \ x_2, \ x_3, \ x_4, \ x_5 \geq 0
\end{align}$$此时 $x = (2,0,0,6,12)$ 目标函数的值为 $-2$
第二次旋转
替入变量为 $x_2$
约束:
- $x_2 = \infty$
- $x_2 = 0$
- $x_2 = 16$
替出变量为 $x_4$ , $x_2 = 4 + \frac{1}{3}x_3 - \frac{2}{3}x_4$
第二次旋转后:
$$\begin{align}
& min \ \ -7 - \frac{1}{6}x_3 + \frac{5}{6}x_4 \\
s.t. \ & x_1 = 3 - \frac{1}{6}x_3 - \frac{1}{6}x_4 \\
& x_2 = 4 + \frac{1}{3}x_3 - \frac{2}{3}x_4 \\
& x_5 = 9 - \frac{3}{2}x_3 + \frac{1}{2}x_4
\end{align}$$此时 $x = (3,4,0,0,9)$ 目标函数的值为 $-7$
第三次旋转
替入变量为 $x_3$
约束:
- $x_3 = 18$
- $x_3 = \infty$
- $x_3 = 0$
替出变量为 $x_5$ , $x_3 = 6 + \frac{1}{3}x_4 - \frac{2}{3}x_5$
第三次旋转后:
$$\begin{align}
& min \ \ -8 + \frac{7}{9}x_4 + \frac{1}{9}x_5 \\
s.t. & \ x_1 = 2 - \frac{2}{9}x_4 + \frac{1}{9}x_5 \\
& x_2 = 6 - \frac{5}{9}x_4 - \frac{2}{9}x_5 \\
& x_3 = 6 + \frac{1}{3}x_4 - \frac{2}{3}x_5
\end{align}$$此时 $x = (2,6,6,0,0)$ 目标函数的值为 $-8$
目标函数中已没有系数为负的项,算法收敛,此时的解为最优解

