SVM回顾
SVM最终的优化目标
$$\begin{align}
& \min_{\alpha} \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_jK(x_i, x_j) - \sum_{i=1}^m \alpha_i \\
& s.t. \ \sum_{i=1}^m\alpha_iy_i = 0, \ 0 \leq \alpha \leq C, \ i \in \lbrace 1,2,…,m \rbrace
\end{align}$$根据KKT互补松弛条件可得:
$$\begin{align}
\alpha_i = 0 \implies y_i(w^Tx_i + b) \geq 1 \\
0 < \alpha_i < C \implies y_i(w^Tx_i + b) = 1 \\
\alpha_i = C \implies y_i(w^Tx_i + b) \leq 1
\end{align}$$
SMO算法理解
属于坐标轮换法 (coordinate descent),即每次只允许一个变量变化,其它变量都视为常数,沿选定变量的坐标方向进行优化。这种方法把多变量优化问题轮流转化成单变量优化问题,在优化过程中不需要目标函数的导数,只需要目标函数的值的信息
由于SVM算法的约束条件 $\sum_{i=1}^m\alpha_iy_i = 0$ ,若每次只优化一个 $\alpha$ 的值,则无法满足该约束条件,因此需要每次针对两个变量进行优化
重复下列过程直至收敛
- 选择下一步要优化的 $\alpha_i$ 和 $\alpha_j$
- 保持其它的 $\alpha$ 的值不变,仅通过改变 $\alpha_i$ 和 $\alpha_j$ 来优化目标函数
假定选择 $\alpha_1, \alpha_2$ 进行优化,为简化表达式,定义 $K_{ij} = K(x_i, x_j) = \phi(x_i) \cdot \phi(x_j)$ ,则本轮需要优化的目标函数如下:
$$\begin{align}
& \min_{\alpha_1,\alpha_2} \ \frac{1}{2} \alpha_1^2K_{11} + \frac{1}{2} \alpha_2^2K_{22} + \alpha_1\alpha_2y_1y_2K_{12} + \alpha_1y_1\sum_{i=3}^m\alpha_iy_iK_{i1} + \alpha_2y_2\sum_{i=3}^m\alpha_iy_iK_{i2} - (\alpha_1 + \alpha_2) \\
& s.t. \ \alpha_1y_1 + \alpha_2y_2 = -\sum_{i=3}^m\alpha_iy_i = \zeta, \ 0 \leq \alpha_i \leq C, \ i \in \lbrace 1,2\rbrace
\end{align}$$根据KKT条件判断是否收敛
SMO算法中 $\alpha$ 的上下界
根据约束条件 $\alpha_1y_1 + \alpha_2y_2 = \zeta$ ,可得 $\alpha_1 = (\zeta - \alpha_2y_2)y_1$ 。由于 $y_1,y_2$ 只能取 $1$ 或 $-1$ ,因此两者关系的斜率只能为 $1$ 或 $-1$
由于$0 \leq \alpha_i \leq C$ ,因此 $\alpha_1,\alpha_2$ 的取值范围为 $[0, C]$
如果 $y_1 = y_2$ ,则 $\alpha_1y_1 + \alpha_2y_2 = \alpha_1 + \alpha_2 = \zeta$
- 当 $\zeta > C$ ,如左图所示,$\max_{\alpha_2} = C, \ \min_{\alpha_2} = \zeta - C = \alpha_1 + \alpha_2 -C$
- 当 $\zeta < C$ ,如右图所示,$\max_{\alpha_2} = \zeta = \alpha_1 + \alpha_2, \ \min_{\alpha_2} = 0$
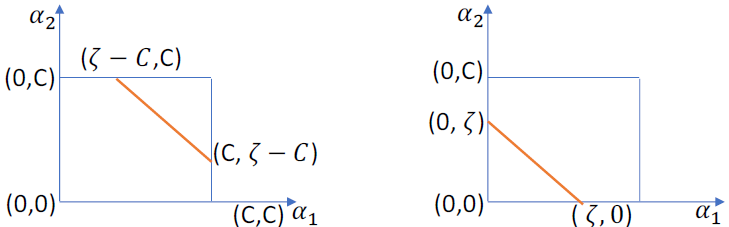
如果 $y_1 \neq y_2$ ,则 $\alpha_1 - \alpha_2 = \zeta$
- 当 $\zeta > 0$ ,如左图所示,$\max_{\alpha_2} = C - \zeta = C - \alpha_1 + \alpha_2, \ \min_{\alpha_2} = 0$
- 当 $\zeta < 0$ ,如右图所示,$\max_{\alpha_2} = C, \ \min_{\alpha_2} = -\zeta = -\alpha_1 + \alpha_2$
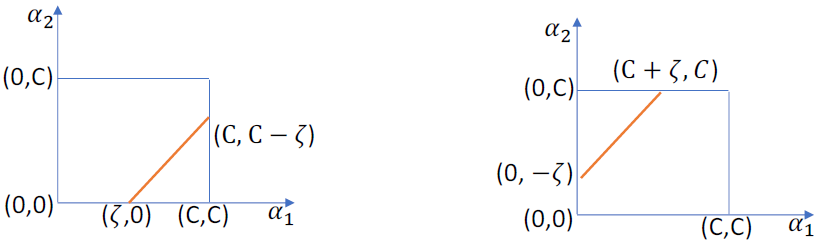
综上可得SMO算法中 $\alpha$ 的上下界:
$$\begin{align}
& if \quad y_1 = y_2: \\
& H = max(C, \alpha_1^{old} + \alpha_2^{old}), \ L = min(0, \alpha_1^{old} + \alpha_2^{old} - C) \\
& if \quad y_1 \neq y_2: \\
& H = max(C, C - \alpha_1^{old} + \alpha_2^{old}), \ L = min(0, \alpha_2^{old} - \alpha_1^{old})
\end{align}$$也就是说,当我们通过求导获得了 $\alpha_2^{new,unclipped}$ ,需要判断其与上下界的关系,对超出上下界的值进行修剪,得到最终的 $\alpha_2^{new}$ :
$$\alpha_2^{new} = \begin{cases}
H, \ \alpha_2^{new,unclipped} > H \\
\alpha_2^{new,unclipped}, \ L \leq \alpha_2^{new,unclipped} \leq H \\
L, \ \alpha_2^{new,unclipped} < L
\end{cases}$$
SMO算法的推导
为简化叙述,定义:
$$\begin{align}
& K_{ij} = K(x_i, x_j) = \phi(x_i) \cdot \phi(x_j) \\
& g(x) = w^* \cdot \phi(x_i) + b^* = \sum_{j=1}^m \alpha_j^*y_jK_{ij} + b^* \\
& E_i = g(x_i) - y_i = \sum_{j=1}^m \alpha_j^*y_jK_{ij} + b^* - y_i \\
& v_i= \sum_{j=3}^m \alpha_jy_jK_{ij} = g(x_i) - \sum_{j=1}^2 \alpha_jy_jK_{ij} - b
\end{align}$$目标函数进一步简化为:
$$W(\alpha_1,\alpha_2) = \frac{1}{2}\alpha_1^2K_{11} + \frac{1}{2}\alpha_2^2K_{22} + \alpha_1\alpha_2y_1y_2K_{12} + \alpha_1y_1v_1 + \alpha_2y_2v_2 - (\alpha_1 + \alpha_2)$$将 $\alpha_1 = (\zeta - \alpha_2y_2)y_1$ 带入目标函数,消去 $\alpha_1$:
$$\begin{align}
W(\alpha_2) & = \frac{1}{2}[(\zeta - \alpha_2y_2)y_1]^2K_{11} + \frac{1}{2}\alpha_2^2K_{22} + (\zeta - \alpha_2y_2)y_1\alpha_2y_1y_2K_{12} + (\zeta - \alpha_2y_2)y_1^2v_1 + \alpha_2y_2v_2 - (\zeta - \alpha_2y_2)y_1 - \alpha_2 \\
& = \frac{1}{2}(\zeta - \alpha_2y_2)^2K_{11} + \frac{1}{2}\alpha_2^2K_{22} + (\zeta - \alpha_2y_2)\alpha_2y_2K_{12} + (\zeta - \alpha_2y_2)v_1 + \alpha_2y_2v_2 - (\zeta - \alpha_2y_2)y_1 - \alpha_2 \\
& = \frac{1}{2}(\zeta - \alpha_2y_2)^2K_{11} + \frac{1}{2}\alpha_2^2K_{22} + \zeta\alpha_2y_2K_{12} - \alpha_2^2K_{12} + (\zeta - \alpha_2y_2)v_1 + \alpha_2y_2v_2 - (\zeta - \alpha_2y_2)y_1 - \alpha_2
\end{align}$$对 $\alpha_2$ 求导,令导数为零,求出极小值:
$$\begin{align}
\frac{\partial W}{\partial \alpha_2} & = -K_{11}(\zeta - \alpha_2y_2)y_2 + K_{22}\alpha_2 + K_{12}\zeta y_2 -2K_{12}\alpha_2 - y_2v_1 + y_2v_2 + y_1y_2 - 1 \\
& = K_{11}\alpha_2 -K_{11}\zeta y_2 + K_{22}\alpha_2 + K_{12}\zeta y_2 -2K_{12}\alpha_2 - y_2v_1 + y_2v_2 + y_1y_2 - 1 \\
& = (K_{11} + K_{22} -2K_{12})\alpha_2 -y_2(K_{11}\zeta - K_{12}\zeta + v_1 - v_2 - y_1 + y_2) \\
& = 0
\end{align}$$得到:
$$\begin{align}
(K_{11} + K_{22} -2K_{12})\alpha_2 & = y_2(K_{11}\zeta - K_{12}\zeta + v_1 - v_2 - y_1 + y_2) \\
& = y_2[K_{11}\zeta - K_{12}\zeta - y_1 + y_2 + g(x_1) - \sum_{j=1}^2\alpha_jy_jK_{1j} - b - (g(x_2) - \sum_{j=1}^2\alpha_jy_jK_{2j} - b)] \\
& = y_2[K_{11}\zeta - K_{12}\zeta - y_1 + y_2 + g(x_1) - \sum_{j=1}^2\alpha_jy_jK_{1j} - (g(x_2) - \sum_{j=1}^2\alpha_jy_jK_{2j})]
\end{align}$$将 $\zeta = \alpha_1y_1 + \alpha_2y_2$ 带入上式:
$$\begin{align}
(K_{11} + K_{22} -2K_{12})\alpha_2^{new,unclipped} & = y_2[K_{11}\zeta - K_{12}\zeta - y_1 + y_2 + g(x_1) - (\alpha_1^{old}y_1K_{11} + \alpha_2^{old}y_2K_{12}) - g(x_2) + (\alpha_1^{old}y_1K_{12} + \alpha_2^{old}y_2K_{22})] \\
& = y_2[K_{11}(\alpha_1^{old}y_1 + \alpha_2^{old}y_2) - K_{12}(\alpha_1^{old}y_1 + \alpha_2^{old}y_2) - y_1 + y_2 + g(x_1) - (\alpha_1^{old}y_1K_{11} + \alpha_2^{old}y_2K_{12}) - g(x_2) + (\alpha_1^{old}y_1K_{12} + \alpha_2^{old}y_2K_{22})] \\
& = y_2[K_{11}\alpha_2^{old}y_2 - 2K_{12}\alpha_2^{old}y_2 + K_{22}\alpha_2^{old}y_2 - y_1 + y_2 + g(x_1) - g(x_2)] \\
& = (K_{11} + K_{22} - 2K_{12})\alpha_2^{old} + y_2(E_1 - E_2)
\end{align}$$$\alpha_2^{new,unclipped}$ 最终的表达式:
$$\alpha_2^{new,unclipped} = \alpha_2^{old} + \frac{y_2(E_1 - E_2)}{K_{11} + K_{22} - 2K_{12}}$$根据 $\alpha$ 的上下界,可以求得 $\alpha_2^{new}$ ,根据 $\zeta = \alpha_1y_1 + \alpha_2y_2$ 可以求得 $\alpha_1^{new}$
更新 $b$ 和 $E$
每轮优化完两个变量后,需要更新参数 $b$ 。当 $0 \leq \alpha_1^{new} \leq C$ ,根据KKT条件可得:
$$y_1 - \sum_{i=1}^m \alpha_1y_1K_{1i} - b_1 = 0$$
因此,$b_1^{new}$ 为:
$$b_1^{new} = y_1 - \sum_{i=3}^m \alpha_iy_iK_{1i} - \alpha_1^{new}y_1K_{11} - \alpha_2^{new}y_2K_{12}$$
此时 $E_1$ 为:
$$E_1 = g(x_1) - y_1 = \sum_{i=3}^m \alpha_iy_iK_{1i} + \alpha_1^{old}y_1K_{11} - \alpha_2^{old}y_2K_{12} + b^{old} - y_1$$
将 $b_1^{new}$ 用 $E_1$ 表示,即:
$$b_1^{new} = -E_1 -y_1K_{11}(\alpha_1^{new} - \alpha_1^{old}) - y_2K_{12}(\alpha_2^{new} - \alpha_2^{old}) + b^{old}$$
同样地,如果 $0 \leq \alpha_2^{new} \leq C$ ,那么:
$$b_2^{new} = -E_2 -y_1K_{12}(\alpha_1^{new} - \alpha_1^{old}) - y_2K_{22}(\alpha_2^{new} - \alpha_2^{old}) + b^{old}$$
最终的 $b^{new}$ 为:
$$b^{new} = \frac{b_1^{new} + b_2^{new}}{2}$$
$E_i^{new}$ 为:
$$E_i^{new} = \sum_{x_j \in SV}\alpha_jy_jK(x_i,x_j) + b^{new} - y_i$$
SV指所有支持向量的集合

