SVM算法

Hard margin SVM

支持向量机 (support vector machine, SVM)是一种二分类算法，其基础模型是在空间中寻找一条分界线，使得两个类别之间的间隔最大，因此也叫作最大间隔分类器 (maximum margin classifier)

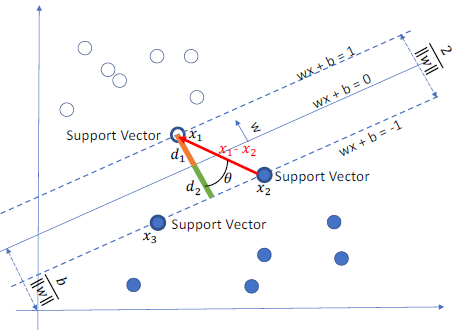
• SVM的决策边界 (decision boundary)可以定义为一个线性方程：$w^TX + b = 0$，其中：

  • $w = {\lbrace w_1,w_2,…,w_n\rbrace}$ 是一个法向量，n是特征的个数

  • $X$ 是训练数据

  • $b$ 是偏置，决定决策边界与原点之间的距离

• SVM用数学公式表示如下：
  $$\begin{cases}
  w^Tx_i + b > 0, \ y_i = 1 \\
  w^Tx_i + b < 0, \ y_i = -1
  \end{cases}$$

将两个式子合并即为：$y_i(w^Tx_i + b) > 0,\ i \in {\lbrace 1,2,…,m \rbrace}$

• 两个类别的训练数据中距离决策边界最近的数据称为支持向量 (support vector)，它们分别位于两条平行于决策边界的线，满足：$w^Tx_i + b = 1$ 或 $w^Tx_i + b = -1$，由此可以推导两个类别之间的间隔：
  $$\begin{align}
  & \because w^Tx_1 + b = 1 \\
  & \quad\ w^Tx_2 +b = -1 \\
  & \therefore (w^Tx_1 + b) - (w^Tx_2 + b) = 2 \\
  & \quad\ w^T(x_1 - x_2) = 2 \\
  & \quad\ w^T(x_1 - x_2) = ||w||_2||x_1 - x_2||_2cos\theta = 2 \\
  & \quad\ d_1 + d_2 = {||x_1 - x_2||}_2cos\theta = \frac {2}{ {||w||}_2}
  \end{align}$$

• 由此可得SVM的目标函数 (objective function)：
  $$\min_{w,b} \frac {1}{2}{||w||_2}^2 \qquad s.t. \ y_i(w^Tx_i + b) \geq 1, \ i \in \lbrace 1,2,…,m\rbrace$$

  约束条件可以写为：$1 - y_i(w^Tx_i + b) \leq 0$

• 将优化问题添加拉格朗日算子：
  $$L(w,b,\alpha) = \frac {1}{2}{||w||2}^2 + \sum{i=1}^m\alpha_i[1 - y_i(w^Tx_i + b)] \qquad s.t. \ \alpha_i \geq 0, \ i \in \lbrace1,2,…,m\rbrace$$

• 原优化问题 (primal problem)等价于：
  $$p^* = \min_{w,b}\max_{\alpha \geq 0} \ L(w,b,\alpha)$$

• 原问题的对偶问题 (dual problem)为：
  $$d^* = \max_{\alpha \geq 0}\min_{w,b} \ L(w,b,\alpha)$$

• 要满足 $p^* = d^*$ (strong duality)，需满足：

  • 优化问题是凸优化 (convex)问题，约束函数是仿射函数 (affine)

  • 满足KKT (Karush-Kuhn-Tucker)条件，即：

    1. $\frac {\partial L}{\partial w} = 0, \ \frac {\partial L}{\partial b} = 0, \ \frac {\partial L}{\partial \alpha} = 0$

    2. $\alpha_i[1 - y_i(w^Tx_i + b)] = 0$

       互补松弛条件，slackness complementary

    3. $\alpha_i \geq 0$

    4. $1 - y_i(w^Tx_i + b) \leq 0$

• 令 $\frac {\partial L}{\partial w} = 0$，可得：
  $$\begin{aligned}
  & \frac {\partial L}{\partial w} = w - \sum_{i=1}^m\alpha_iy_ix_i = 0 \\
  & w^* = \sum_{i=1}^m\alpha_iy_ix_i
  \end{aligned}$$

• 令 $\frac {\partial L}{\partial b} = 0$，可得：
  $$\begin{aligned}
  \frac {\partial L}{\partial b} = -\sum_{i=1}^m\alpha_iy_i = 0
  \end{aligned}$$

• 将上述两个式子带入拉格朗日函数，消去 $w$ 和 $b$，求得 $\min_{w,b} \ L(w,b,\alpha)$：
  $$\begin{aligned}
  & L(\alpha) = \frac {1}{2} \sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^m\alpha_iy_i[\sum_{j=1}^m(\alpha_jy_jx_j) \cdot x_j + b] + \sum_{i=1}^m\alpha_i \\
  & \qquad \ = -\frac {1}{2} \sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) + \sum_{i=1}^m\alpha_i
  \end{aligned}$$

• 原问题转为：
  $$\max_\alpha \ -\frac {1}{2} \sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) + \sum_{i=1}^m\alpha_i \quad s.t. \sum_{i=1}^m\alpha_iy_i = 0, \ \alpha_i \geq 0, \ i \in \lbrace 1,2,…,m\rbrace$$

• 将上面的式子加负号，变成最小化问题：
  $$\min_\alpha \ \frac {1}{2} \sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^m\alpha_i \quad s.t. \sum_{i=1}^m\alpha_iy_i = 0, \ \alpha_i \geq 0, \ i \in \lbrace 1,2,…,m\rbrace$$

  通过序列最小优化算法 (sequential minimal optimiztion, SMO)可以求解 $\alpha$

• 对任意训练样本 $(x_i,y_i)$，总有 $\alpha_i = 0$ 或者 $y_i(w^Tx_i + b) = 1$

  • 若 $\alpha_i = 0$，则该训练样本不必在最终的优化问题中进行计算

  • 若 $\alpha_i > 0$，则 $y_i(w^Tx_i + b) = 1$，该训练样本为支持向量

支持向量机的重要性质：训练完成后，大部分训练数据不需要保留，最终的模型只与支持向量有关

Soft margin SVM

Hard margin SVM适用于训练数据完全线性可分的情况，但在实际情况下，训练数据一般存在一些异常值，使得两个类别并不完全线性可分。Soft margin SVM引入一个松弛变量 $\xi_i$ ，用来表征第 $i$ 个训练样本偏离正确分类的程度。同时引入一个超参数 (hyperparameter) $C$ ，用来控制对这些异常点进行惩罚的程度

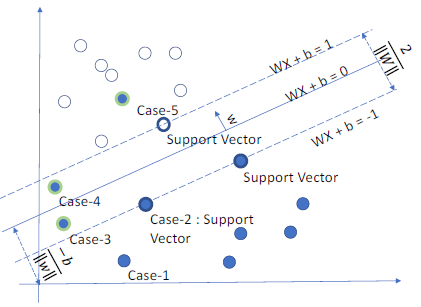
• 带松弛变量的目标函数：
  $$\min_{w,b,\xi} ; \frac {1}{2}{||w||2}^2 + C\sum{i=1}^m\xi_i \quad s.t. \ y_i(w^Tx_i + b) \geq 1 - \xi_i, \ C > 0, \ \xi_i \geq 0, \ i \in \lbrace 1,2,…,m\rbrace$$

  不等式约束：$1 - \xi_i - y_i(w^Tx_i + b) \leq 0$ ; $-\xi_i \leq 0$

• 将目标函数添加拉格朗日算子：
  $$\begin{aligned}
  & L(w,b,\xi,\alpha,\lambda) = \frac {1}{2}{||w||2}^2 + C\sum{i=1}^m\xi_i + \sum_{i=1}^m\alpha_i[1 - \xi_i - y_i(w^Tx_i + b)] - \sum_{i=1}^m\lambda_i\xi_i \\
  & s.t. \ y_i(w^Tx_i + b) \geq 1 - \xi_i, \ C > 0, \ \xi_i \geq 0, \ \alpha_i \geq 0, \ \lambda_i \geq 0, \ i \in \lbrace 1,2,…,m\rbrace
  \end{aligned}$$

• 原优化问题 (primal problem)等价于：
  $$p^* = \min_{w,b,\xi \geq 0} \ \max_{\alpha \geq 0, \lambda \geq 0} \ L(w,b,\xi,\alpha,\lambda)$$

• 原问题的对偶问题 (dual problem)为：
  $$d^* = \max_{\alpha \geq 0, \lambda \geq 0} \ \min_{w,b,\xi \geq 0} \ L(w,b,\xi,\alpha,\lambda)$$

• 令 $\frac {\partial L}{\partial w} = 0$，可得：
  $$\begin{aligned}
  & \frac {\partial L}{\partial w} = w - \sum_{i=1}^m\alpha_iy_ix_i = 0\\
  & w^* = \sum_{i=1}^m\alpha_iy_ix_i
  \end{aligned}$$

• 令 $\frac {\partial L}{\partial b} = 0$，可得：
  $$\begin{aligned}
  & \frac {\partial L}{\partial b} = -\sum_{i=1}^m\alpha_iy_i = 0 \\
  & \sum_{i=1}^m\alpha_iy_i = 0
  \end{aligned}$$

• 令 $\frac {\partial L}{\partial \xi} = 0$，可得：
  $$C - \alpha_i - \lambda_i = 0$$

• 将上述三个式子带入拉格朗日函数，消去 $w$ ，$b$ 和 $\xi$ ：
  $$\begin{aligned}
  & L(\alpha,\lambda) = \frac {1}{2} \sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) + C\sum_{i=1}^m\xi_i + \sum_{i=1}^m\alpha_i - \sum_{i=1}^m\alpha_i\xi_i - \sum_{i=1}^m\alpha_iy_i[\sum_{j=1}^m(\alpha_jy_jx_j) \cdot x_i + b] - \sum_{i=1}^m\lambda_i\xi_i \\
  & \qquad \quad \ = -\frac {1}{2} \sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) + \sum_{i=1}^m\alpha_i + \sum_{i=1}^m\xi_i(C - \alpha_i - \lambda_i) \\
  & \qquad \quad \ = -\frac {1}{2} \sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) + \sum_{i=1}^m\alpha_i
  \end{aligned}$$

• 原问题转为：
  $$\begin{aligned}
  & \max_{\alpha,\lambda} \ -\frac {1}{2} \sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) + \sum_{i=1}^m\alpha_i \\
  & s.t. \ \sum_{i=1}^m\alpha_iy_i = 0, \ C - \alpha_i - \lambda_i = 0 \\
  & \qquad \alpha_i \geq 0, \ \lambda_i \geq 0, \ i \in \lbrace 1,2,…,m \rbrace
  \end{aligned}$$

  由于 $\lambda_i \geq 0$ ，$C - \alpha_i - \lambda_i = 0$ 也可写为 $\alpha_i \leq C$

• 将上面的式子加负号，变成最小化问题：
  $$\begin{aligned}
  & \min_{\alpha,\lambda} \ \frac {1}{2} \sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^m\alpha_i \\
  & s.t. \ \sum_{i=1}^m\alpha_iy_i = 0, \ 0 \leq \alpha_i \leq C, \ \lambda_i \geq 0, \ i \in \lbrace 1,2,…,m \rbrace
  \end{aligned}$$

• 对KKT互补松弛条件的理解：
  $$\begin{cases}
  \alpha_i(1 - \xi_i - y_i(w^Tx_i + b)) = 0 \\
  \lambda_i\xi_i = (C - \alpha_i)\xi_i = 0
  \end{cases}$$

1. 若 $\alpha_i = 0$ ，则 $\xi_i = 0$ ，$y_i(w^Tx_i + b) \geq 1$

   $\alpha_i = 0$ 则对应样本不是支持向量；$\xi_i = 0$ 说明对应样本分类正确

2. 若 $\alpha_i = C$ ，则 $\xi_i \geq 0$ ，$y_i(w^Tx_i + b) \leq 1$

   若 $\xi_i = 0$ 则对应样本分类正确，若 $\xi_i > 0$ 则对应样本偏离正确分类；$\alpha_i \neq 0$ 说明对应样本是支持向量，这一类称为边界支持向量 (bounded SV)

3. 若 $0 < \alpha_i < C$ ，则 $\xi_i = 0$ ，$y_i(w^Tx_i + b) = 1$

   $\xi_i = 0$ 说明对应样本分类正确；$\alpha_i \neq 0$ 说明对应样本是支持向量，这一类称为自由支持向量 (free SV)

合页损失函数 (Hinge lost)

由 $y_i(x^Tx_i + b) \geq 1 - \xi_i$ 可得： $\xi_i \geq 1 - y_i(w^Tx_i + b)$ ；
又由于 $\xi_i \geq 0$ ，$\xi_i = max(0, 1 - y_i(w^Tx_i + b))$ ，称为合页损失函数

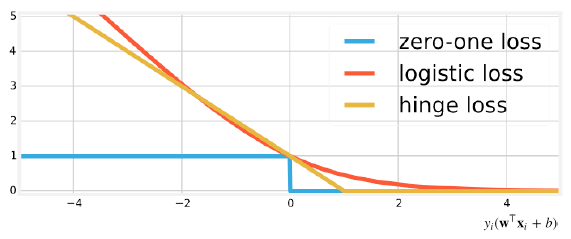
合页损失函数的优点：

• 凸函数，易优化
• 在自变量小于0的部分梯度较小，对错误的惩罚较轻
• 在自变量大于1的部分值为0，即：只要对某个数据分类正确，则不再针对该数据进行优化

Kernel SVM

通过添加松弛变量，可以将一定程度上线性不可分的数据使用SVM进行分类预测；而对于完全线性不可分的数据，可以通过增加数据的维度，将数据映射到高维空间，使其在高维空间中线性可分

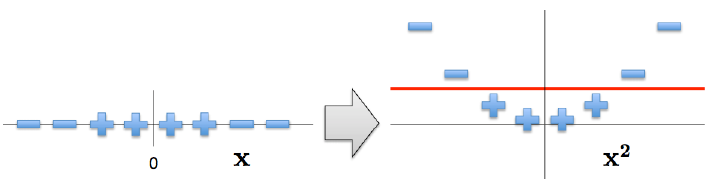
例如：定义 $\phi(x) = x^2$ ，则将 $x_i$，$x_j$ 映射到 $\phi(x)$ 所在的空间后，目标函数 $\min_\alpha \ \frac {1}{2} \sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_i \cdot x_j) - \sum_{i=1}^m\alpha_i$ 变为：
$$\min_\alpha \ \frac {1}{2} \sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(\phi(x_i) \cdot \phi(x_j)) - \sum_{i=1}^m\alpha_i$$

如果直接将数据扩展到高维再计算内积，计算量非常大；且数据不可能扩展到无限维。因此使用 核技巧 (kernel trick) 解决该类问题

设计一个核函数 $K(x_i,x_j) = \phi(x_i) \cdot \phi(x_j)$，即数据 $x_i,x_j$ 在原始低维空间通过核函数 $K(x)$ 运算的结果等于数据 $x_i,x_j$ 映射到高维空间中的内积 $\phi(x_i) \cdot \phi(x_j)$ ，从而极大地降低计算的复杂度

• 使用核函数的预测公式
  $$\begin{aligned}
  & b = y_j - \sum_{i=1}^m\alpha_iy_iK(x_i,x_j) \\
  & \hat y = x^T \phi(x) + b = \sum_{i=1}^m \alpha_iy_iK(x_i,x) + b
  \end{aligned}$$

• 成为核函数的条件：Mercer定理

  任何半正定的对称函数都可以作为核函数

常用的核函数

• 多项式核 (polynomial kernel)
  $$K(x_i,x_j) = ((x_i \cdot x_j) + c)^d$$

  $c \geq 0$ 控制低阶项的强度；当 $c = 0, d = 1$ 时即为线性核 (linear kernel)，相当于没有核函数

• 高斯核 (Gaussian kernel)也叫作Radial Basis Function (RBF) kernel
  $$K(x_i,x_j) = exp(-\frac {||x_i - x_j||_2^2}{2\sigma^2})$$

  使用高斯核之前必须将数据进行标准化

• Sigmoid Kernel
  $$K(x_i,x_j) = tanh(\alpha x_i^Tx_j + c)$$

  相当于一个没有隐藏层 (hidden layer)的简单神经网络

• cosine similarity Kernel
  $$K(x_i,x_j) = \frac {x_i^Tx_j}{||x_i|| \ ||x_j||}$$

  常用于衡量两段文字的相似性；相当于两个向量的余弦相似度

• Chi-squared Kernel
  $$K(x_i,x_j) = 1 - \sum_{i,j}^m \frac {(x_i - x_j)^2}{0.5(x_i + x_j)}$$

  常用于计算机视觉；衡量两个概率分布的相似性；输入数据必须是非负的，且必须使用了L1标准化 (L1 normalized)