一句话评价
- 数学基础深厚
- 对涉及的算法进行了适度解释
- 提供了针对不同类型数据进行特征工程的思路
文章信息
- 题目:Machine Learning Reveals Missing Edges and Putative Interaction Mechanisms in Microbial Ecosystem Networks
- 单位:波士顿大学
- DOI:10.1128/mSystems.00181-18
- 杂志:mSystems (IF 6.633)
- 分类:Research article
要解决的问题
提出了用数学方法表征微生物相互作用的概念框架,并应用于三个实例:
三个实例都有菌株两两共培养的实验数据
- 100个人肠道细菌代谢模型的模拟群落
- 包含14个菌株的大肠杆菌氨基酸营养缺陷型群落
- 分离自同一土壤样品的20个微生物组成的群落
实验设计
特征工程
对于给定群落
C,菌株i在菌株j存在时的响应记为群落矩阵 $X$ 中的 $X_{ij}$ 元素$X_{ij}$ 代表共培养结束时菌株
i的标准化丰度或者与菌株j共培养是否能够存活的0-1数据对
C中的每一个菌株i定义一个包含n个特征的特征向量 $F^{(i)}$,包含是否存在特定基因、代谢功能等$F_k^{(i)}$ 根据特征
k是否存在于菌株i记为1或0每一对菌株(i, j)关联一个串联特征向量 $F^{(i,j)} = [F^{(i)},F^{(j)}]$
一般情况下,$F^{(i,j)} \neq F^{(j,i)}$ 且 $X_{ij} \neq X_{ji}$
肠道微生物相互作用数据
数据来自已发表的文章[1]
流平衡分析 (flux balance analysis, FBA),是一种基于约束的稳态模型[2,3,4,5]
根据基因组注释构建代谢网络
利用代谢网络构建化学计量矩阵
S$S_{ij}$ 元素表示通过反应
j消耗或产生了几分子的i基于稳态假设,根据边界约束条件定义环境中营养物质的可获得性
约束来自两个方面:能量守恒等物理规律及底物的供应等客观限制。这个步骤是确定约束条件和目标函数的过程
通过线性优化获得使生物量最大的流分布
动态流平衡分析 (dynamic flux balance analysis, dFBA):仍然假设细胞内的代谢物处于稳态,但环境中总的生物量和代谢物视作时间依赖的变量
使用之前已发表的
COMETS平台进行仿真[6]选择了100个代谢模型 (菌株)
设置所有菌株单独培养都能生长的培养基
两两共培养仿真设置为混合良好的分批培养 (batch culture)
如果 $B_{ij}$ 是菌株
i在与菌株j共培养时最终的生物量,$B_{ii}$ 是菌株i单独培养时最终的生物量,定义 $X_{ij} = \frac {B_{ij} - B_{ii}} {B_{ii}}$如果$X_{ij} < 0$,表明菌株
i受菌株j抑制;如果$X_{ij} = 0$,表明菌株j对菌株i没有影响
本例中特征向量 $F^{(i)}$ 定义为物种
i的基因组中是否存在 (1 / 0)化学计量矩阵S中的194个可能的反应基于两个特征向量 $F^{(i)}$ 和 $F^{(j)}$ 之间的
Jaccard距离的分类器用于与随机森林模型进行比较,定义为:
$$ JD(F^{(i)},F^{(j)}) = 1 - \frac {F^{(i)} \bigcap F^{(j)}} {F^{(i)} \bigcup F^{(j)}} $$
营养缺陷型大肠杆菌数据
数据来自已发表的文章[7]
通过基因敲除获得14个氨基酸营养缺陷型大肠杆菌菌株
共培养使用M9葡萄糖培养基200 μl体系,30 ℃培养84 h
通过菌落计数、qPCR确定菌株比例
本例中特征向量 $F^{(i)}$ 定义为是否能合成14种氨基酸,共培养表型 $X_{ij}$ 定义为菌株
i在与菌株j共培养时,最终生物量变化的倍数
土壤群落数据
数据来自已发表的文章[8]
菌株的存活通过5轮稀释后进行菌落计数及高通量测序获得
为构建特征向量 $F^{(i)}$,从GenBank下载各菌株的16S rRNA序列,用PICRUSt预测其KEGG模块。其中18个菌株通过预测获得了KEGG模块,将特征向量定义为是否存在79个KEGG模块
$X_{ij}$ 定义为菌株
i与菌株j共培养时能否存活
随机森林建模
使用
RandomForestR包使用默认参数
根据训练集的
OOB及5-倍交叉验证评估准确率,绘制ROC曲线使用
forestFloorR包计算特征对分类的贡献
数据及代码
https://github.com/ddimucci/MicrobialCommunities
结果
表征两两相互作用
特征向量可以通过串联各种生物学相关特征进行构建,如:是否编码特定基因或代谢功能、系统发育地位、发现该微生物的环境等
这些特征向量结合已知的相互作用关系可以用来训练机器学习模型,进而预测未观察到的相互作用
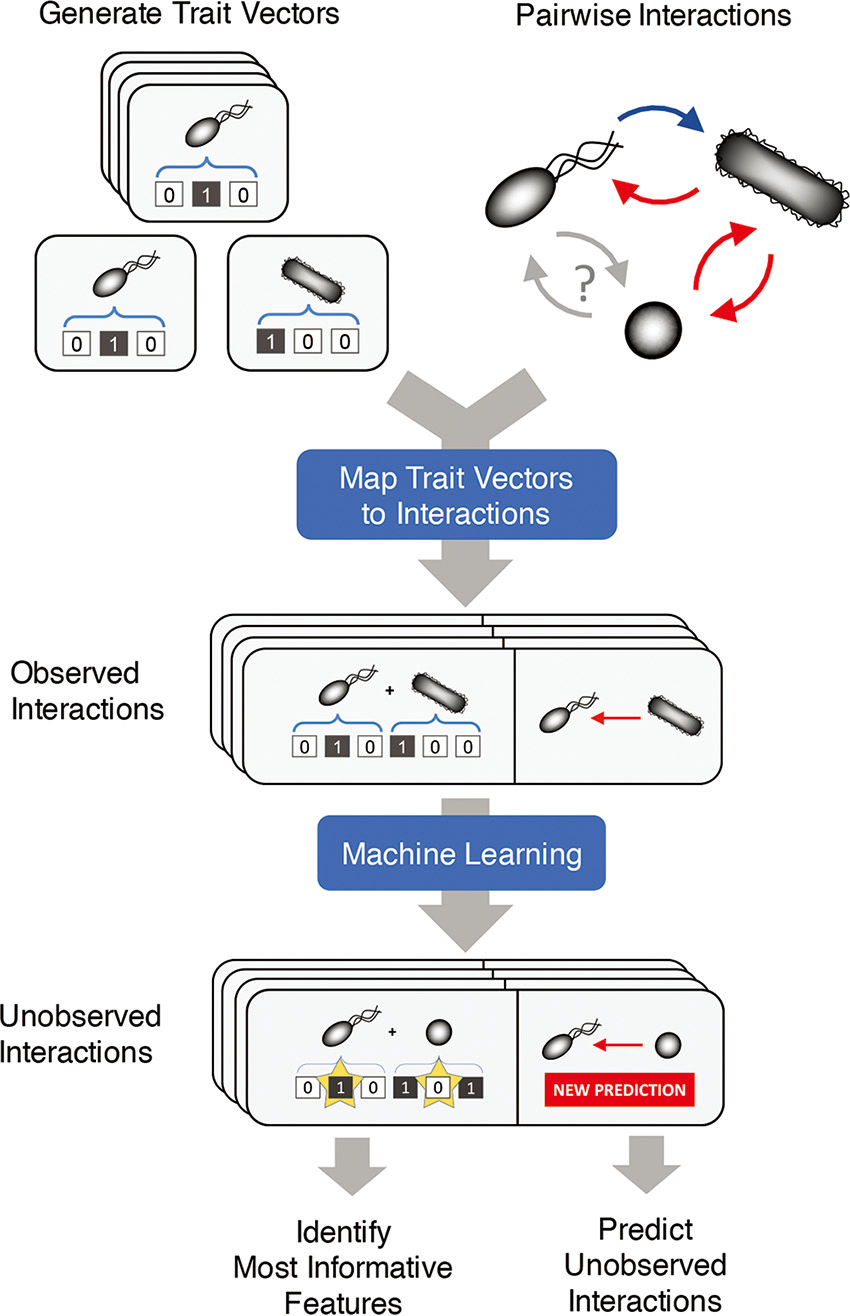
在计算机预测的人肠道微生物相互作用数据中的应用
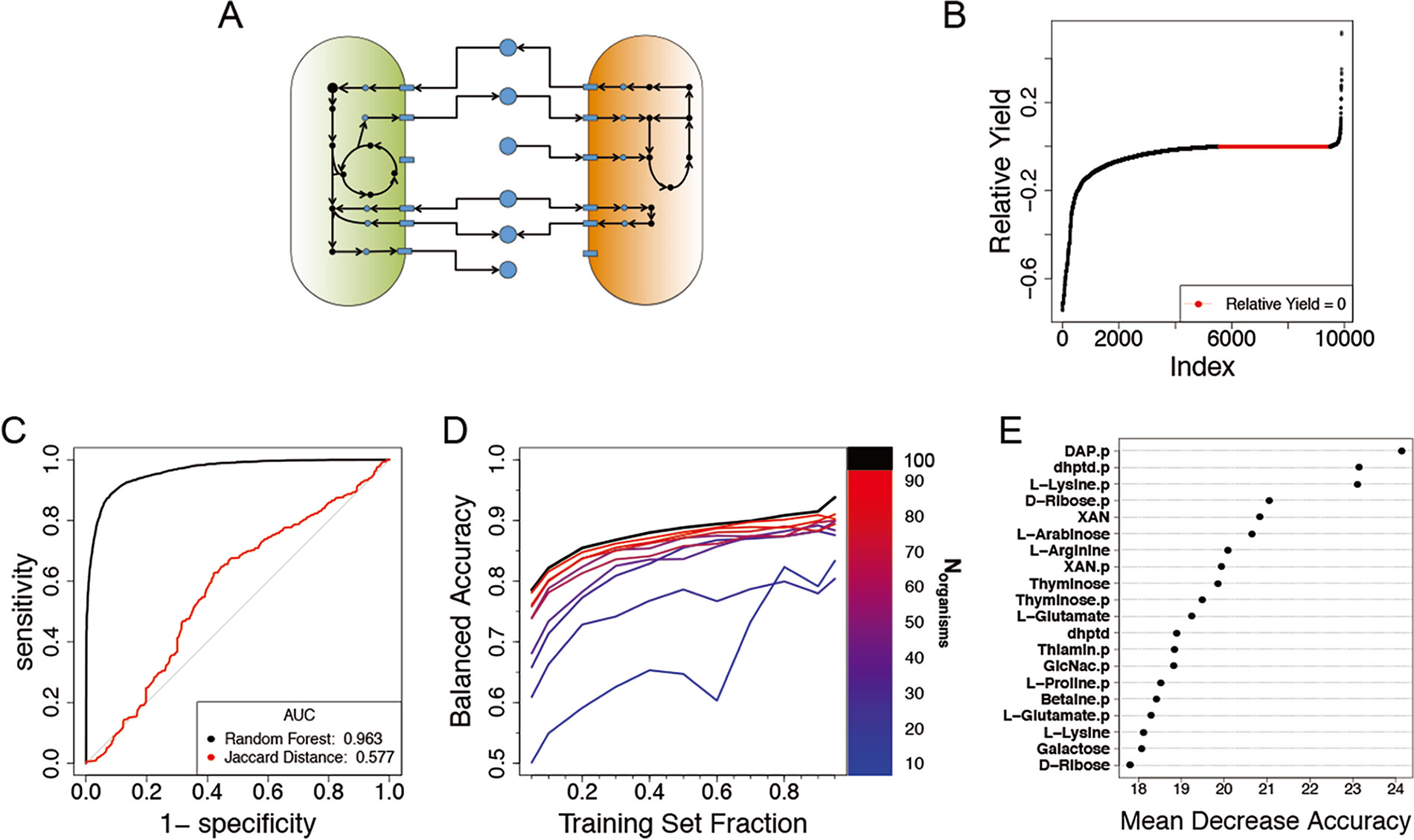
特征向量为每个菌株是否编码各种营养物质交换反应的基因 (图2A)
仿真实验表型为菌株两两共培养最终的生物量相对变化 (图2B)
5,563个样本的最终相对生物量减少,3,917个样本的最终相对生物量基本不变,420个样本的最终相对生物量增加
对整个数据集进行训练,准确率约为90.5%。ROC曲线表明随机森林模型比单纯根据
Jaccard距离预测负相互作用效果更好 (图2C)通过绘制学习曲线判断群落大小及训练数据的多少对准确率的影响:群落越大,达到较高准确率需要的训练数据(实验结果)越少 (图2D)
获得了最重要的20个特征 (图2E)
纵坐标的p上标表示该特征是属于共培养对象的
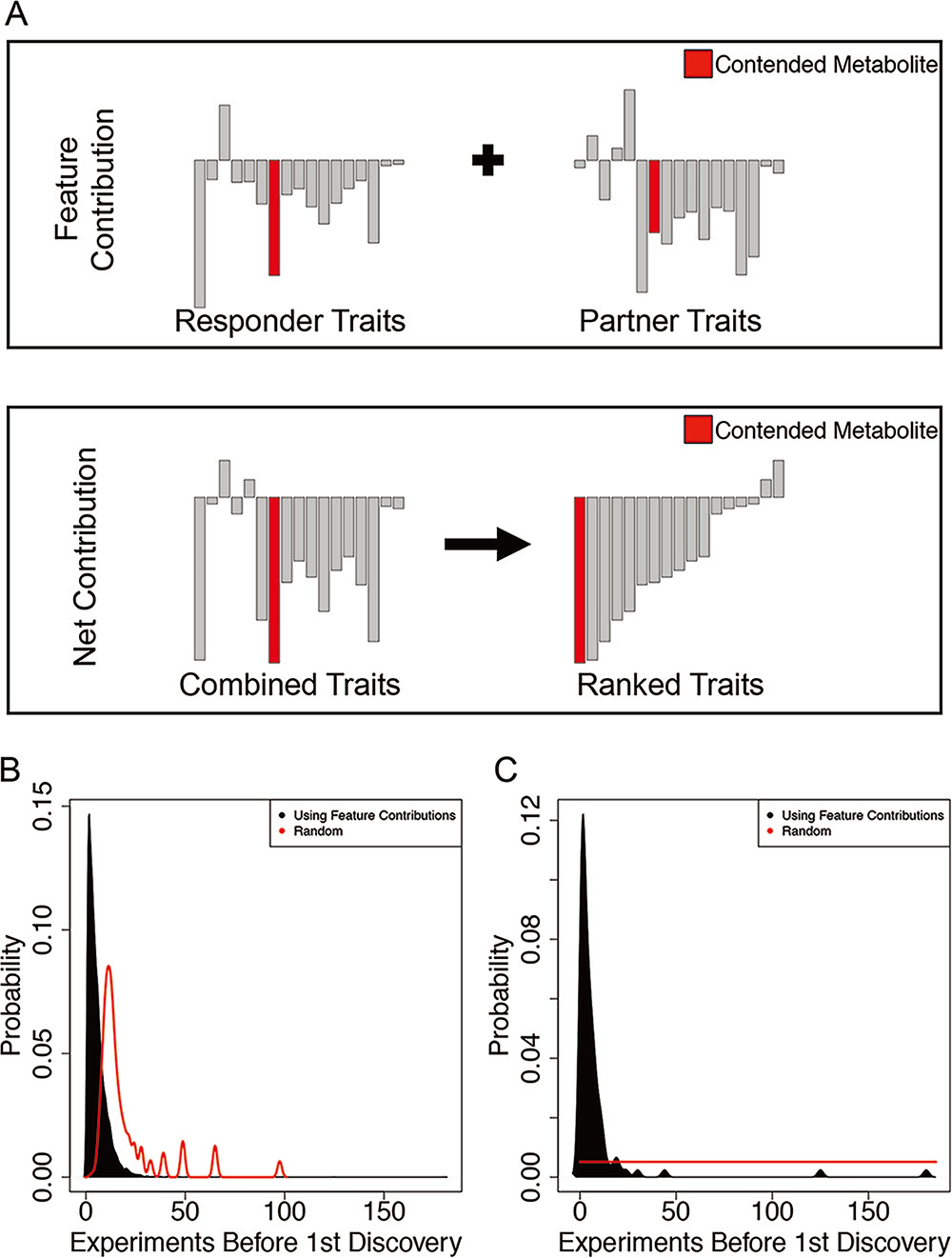
- 随机森林模型还可定量计算特定变量对单个样品的分类有多大影响,从而用于推测相互作用的机制 (图3)
在营养缺陷型大肠杆菌数据中的应用
任意两个菌株的相互作用依赖于直接的缺陷氨基酸交换 (图4A)
利用共培养的最终生长倍数变化构建表型矩阵,以变化2倍作为“强相互作用”和“弱相互作用”的阈值 (图4B)
随机森林模型的准确率约为79.2%,根据ROC曲线,表现比基于生物合成代价矩阵的预测更好 (图4C)
变量重要性分析表明,缺陷的氨基酸对于分类的准确率影响更大 (图4E)
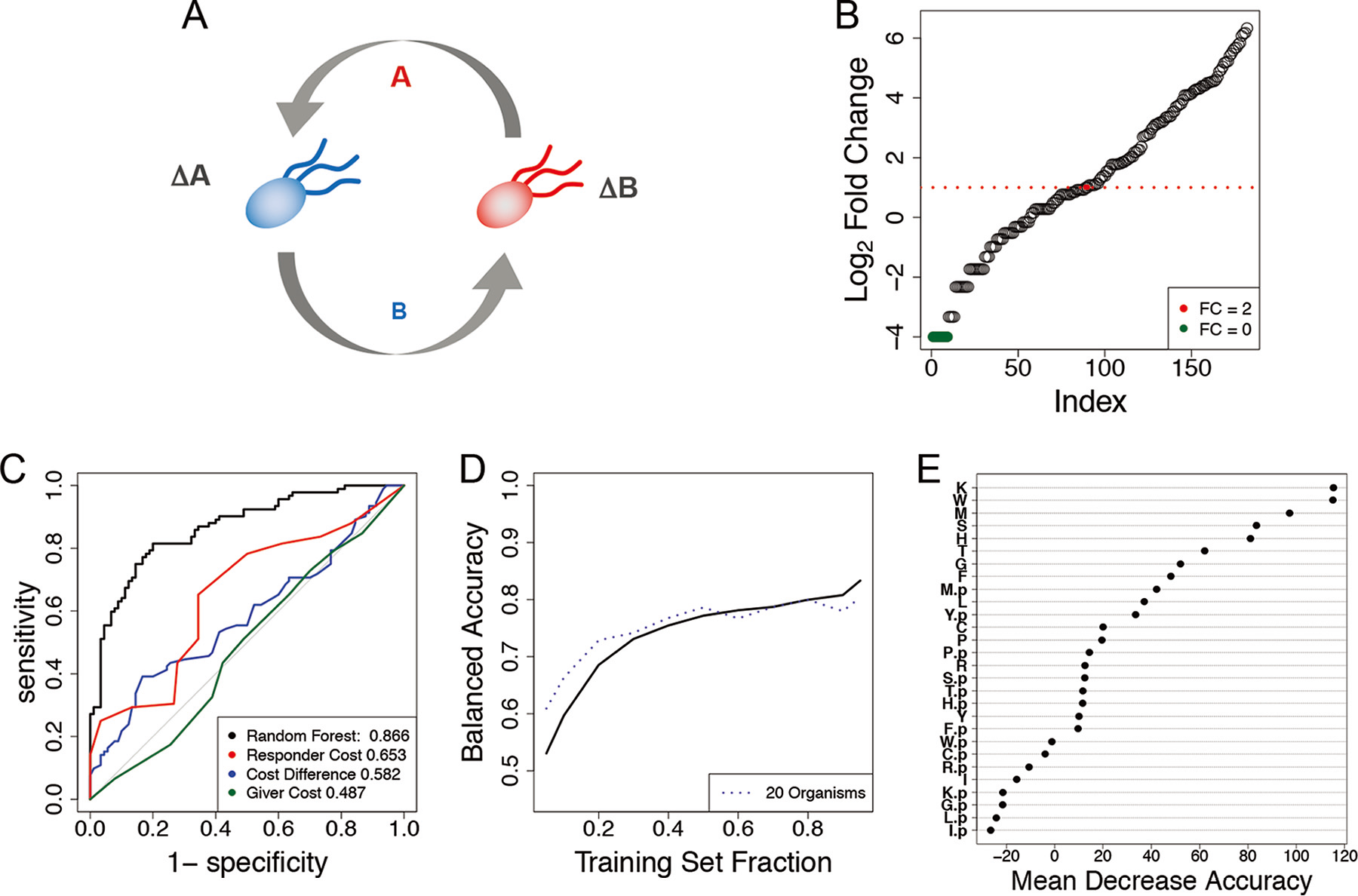
- 对特征贡献的分析发现,缺失某种氨基酸对随机森林分类器的影响比存在某种氨基酸更大
在土壤细菌群落数据中的应用
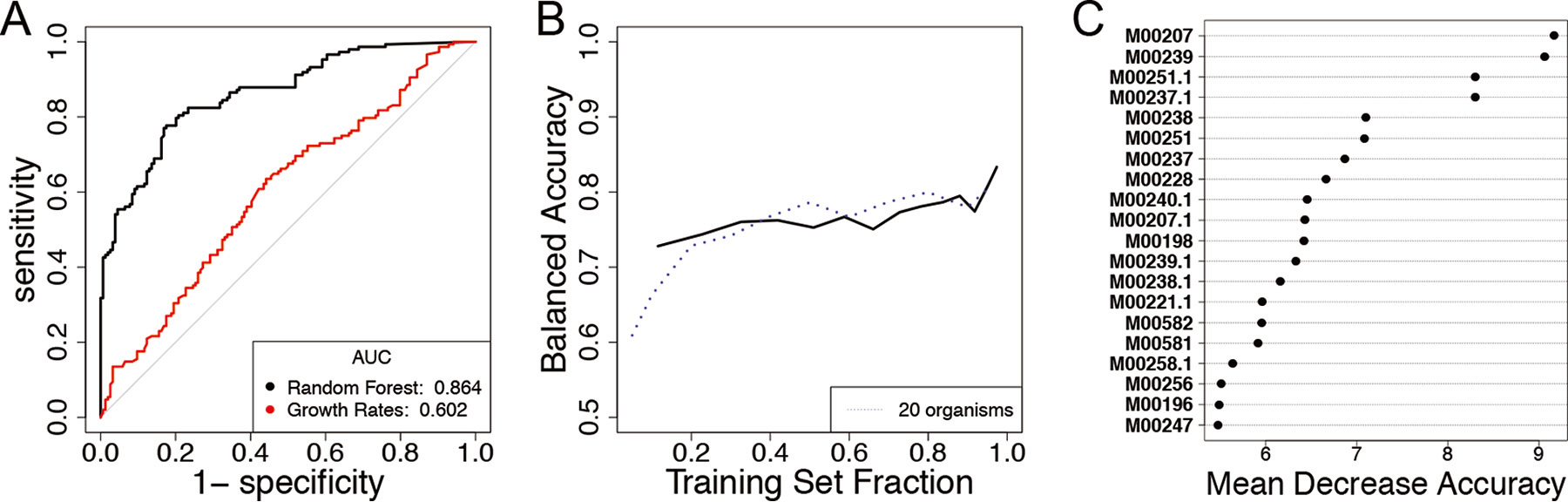
随机森林模型准确率约为79.4%
ROC曲线表明随机森林模型表现比根据初始生长速率的预测效果更好 (图5A)
学习曲线趋势与基于仿真数据的趋势一致 (图5B)
参考文献
[1] Bauer E, Laczny CC, Magnusdottir S, Wilmes P, Thiele I. 2015. Phenotypic differentiation of gastrointestinal microbes is reflected in their encoded metabolic repertoires. Microbiome 3:55.
[2] Maarleveld TR, Khandelwal RA, Olivier BG, Teusink B, Bruggeman FJ. 2013. Basic concepts and principles of stoichiometric modeling of metabolic networks. Biotechnol J 8:997–1008.
[3] Raman K, Chandra N. 2009. Flux balance analysis of biological systems: applications and challenges. Brief Bioinform 10:435– 449.
[4] O’Brien EJ, Monk JM, Palsson BO. 2015. Using genome-scale models to predict biological capabilities. Cell 161:971–987.
[5] Orth JD, Thiele I, Palsson BØ. 2010. What is flux balance analysis? Nat Biotechnol 28:245–248.
[6] Harcombe WR, Riehl WJ, Dukovski I, Granger BR, Betts A, Lang AH, Bonilla G, Kar A, Leiby N, Mehta P, Marx CJ, Segrè D. 2014. Metabolic resource allocation in individual microbes determines ecosystem interactions and spatial dynamics. Cell Rep 7:1104–1115.
[7] Mee MT, Collins JJ, Church GM, Wang HH. 2014. Syntrophic exchange in synthetic microbial communities. Proc Natl Acad Sci U S A 111: E2149–E2156.
[8] Higgins LM, Friedman J, Shen H, Gore J. 2017. Co-occurring soil bacteria exhibit a robust competitive hierarchy and lack of non-transitive interactions. bioRxiv
